problem
stringlengths 2
1.73k
| answer
stringlengths 1
313
| solution
stringlengths 3
9.24k
| difficulty
float64 1
10
|
|---|---|---|---|
6. In the Kingdom of Mathematics, the denominations of banknotes in circulation are 1 yuan, 5 yuan, 10 yuan, 20 yuan, 50 yuan, and 100 yuan. One day, two customers each bought a chocolate bar worth 15 yuan at the same grocery store. One of them paid with two 10-yuan banknotes, while the other paid with a 20-yuan and a 5-yuan banknote. When settling the accounts, the boss only needed to give one 10-yuan banknote from the first person to the second person, and then give the 5-yuan banknote from the second person to the first person. One day, two more customers came to buy chewing gum of the same price, and a similar situation occurred as before, where both paid more than the price. The boss only needed to give part of the first person's payment to the second person, and then give part of the second person's payment to the first person. Therefore, ( ) is a possible price for the chewing gum.
(A) 2 yuan
(B) 6 yuan
(C) 7 yuan
(D) 8 yuan
|
8
|
【Answer】D
【Analysis】Considering the four cases respectively, when the gum costs 8 yuan, one person pays 10 yuan (2 five-yuan notes), and another person pays 13 yuan (1 ten-yuan note, 3 one-yuan notes), the first person's 1 five-yuan note can be given as change to the second person, and the second person's 2 one-yuan notes can be given as change to the first person, thus completing the change. The other cases do not meet the requirements of the problem, so the answer is D.
| 4.67
|
4. Triples of natural numbers $\left(a_{i}, b_{i}, c_{i}\right)$, where $i=1,2, \ldots, n$ satisfy the following conditions:
1) $a_{i}+b_{i}+c_{i}=2017$ for all $i=1,2, \ldots, n$;
2) if $i \neq j$, then $a_{i} \neq a_{j}, b_{i} \neq b_{j}$ and $c_{i} \neq c_{j}$. What is the maximum possible value of $n$? (M. Popov)
|
1343
|
Answer: 1343.
Solution: Note that
$$
\sum_{i=1}^{n} a_{i} \geqslant \sum_{i=1}^{n} i=\frac{n(n+1)}{2} .
$$
A similar inequality is written for the sums $b_{i}$ and $c_{i}$. Adding the three obtained inequalities, we get
$$
\begin{gathered}
3 \cdot \frac{n(n+1)}{2} \leqslant \sum_{i=1}^{n} a_{i}+\sum_{i=1}^{n} b_{i}+\sum_{i=1}^{n} c_{i}= \\
=\sum_{i=1}^{n}\left(a_{i}+b_{i}+c_{i}\right)=2017 n .
\end{gathered}
$$
Thus, we obtain the upper bound
$$
\frac{3(n+1)}{2} \leqslant 2017 \Longrightarrow n \leqslant 1343
$$
Now let's provide an example where this bound is achieved ( $n=1343$ )
| $a_{i}$ | $b_{i}$ | $c_{i}$ |
| :---: | :---: | :---: |
| 1 | 672 | 1344 |
| 2 | 673 | 1342 |
| $\vdots$ | $\vdots$ | $\vdots$ |
| 672 | 1343 | 2 |
| 673 | 1 | 1343 |
| 674 | 2 | 1341 |
| $\vdots$ | $\vdots$ | $\vdots$ |
| 1343 | 671 | 3 |
| 4.67
|
5. What is the maximum number of rooks that can be placed on the cells of a $300 \times 300$ board so that each rook attacks no more than one other rook? (A rook attacks all cells it can reach according to chess rules, without passing through other pieces.)
#
|
400
|
# Answer: 400
First solution. We will prove that no more than 400 rooks can be placed on the board. In each row or column, there are no more than two rooks; otherwise, the rook that is not at the edge will attack at least two other rooks. Suppose there are $k$ columns with two rooks each. Consider one such pair. They attack each other, so there are no rooks in the rows where they are located. Thus, rooks can only be in $300-2k$ rows. Since there are no more than two rooks in each of these rows, the total number of rooks is no more than $2(300-2k) + 2k = 600 - 2k$. On the other hand, in $k$ columns, there are two rooks each, and in the remaining $300-k$ columns, there is no more than one rook, so the total number of rooks is no more than $(300-k) + 2k = 300 + k$. Therefore, the total number of rooks is no more than $\frac{1}{3}((600-2k) + 2(300+k)) = 400$.
Next, we will show how to place 400 rooks. On a $3 \times 3$ board, 4 rooks can be placed as shown in the figure, and then 100 such squares can be placed along the diagonal.
Second solution. On the board, there can be rooks that do not attack any other rooks, as well as pairs of rooks that attack each other. Let there be $k$ single rooks and $n$ pairs of rooks that attack each other. Then the total number of rooks on the board is $k + 2n$. We will count the total number of occupied rows and columns (for convenience, we will call them lines). Each single rook occupies its own row and its own column, i.e., two lines. Each pair of rooks occupies three lines. Therefore, the total number of lines occupied is $2k + 3n$. Thus, $2k + 3n \leq 600$. Therefore, $k + 2n = \frac{2}{3}(2k + 3n) - \frac{k}{3} \leq \frac{2}{3}(2k + 3n) \leq \frac{2}{3} \cdot 600 = 400$.
The example of placement is the same as in the first solution.
| 5
|
4. A kilo of sausages was placed on a straight line between a dog in a kennel and a cat. The animals simultaneously rushed to the sausages. The cat runs twice as fast as the dog, but eats twice as slowly. Upon reaching the sausages, both ate without fighting and ate an equal amount. It is known that the cat could eat all the sausages in one minute and also run from the starting point to the dog's kennel in one minute. To whom were the sausages placed closer, and by how many times?
|
1.4
|
Answer: 1.4 times closer to the dog than to the cat.
## Solution:
Let $v$ be the running speed of the dog, $u$ be the eating speed of the cat, and the volume of sausages eaten by each animal be 1.
Then, $2 v$ is the running speed of the cat, and $2 u$ is the eating speed of the dog.
Let the distance from the cat to the sausages be $x$, and the distance from the dog's kennel to the sausages be $-y$.
The total time from the start of movement to the end of eating sausages is the same for both the cat and the dog, i.e., $x / 2 v + 1 / u = y / v + 1 / 2 u$.
According to the condition, we have: $2 / u = (x + y) / 2 v$.
Substituting $1 / u$ and $1 / 2 u$ in the first equation with $(x + y) / 4 v$ and $(x + y) / 8 v$ respectively, derived from the second equality,
we get $x / 2 v + (x + y) / 4 v = y / v + (x + y) / 8 v$.
Multiplying by $8 v$, we have: $4 x + 2(x + y) = 8 y + (x + y)$.
Combining like terms, we finally get: $5 x = 7 y$, hence the answer.
## Instructions for Checking:
Answer without justification but with verification - 2 points.
Answer without verification - 1 point.
| 2
|
Compute the smallest positive integer that does not appear in any problem statement on any round at HMMT November 2023.
|
22
|
The number 22 does not appear on any round. On the other hand, the numbers 1 through 21 appear as follows. \begin{tabular}{c|c|c} Number & Round & Problem \\ \hline 1 & Guts & 21 \\ 2 & Guts & 13 \\ 3 & Guts & 17 \\ 4 & Guts & 13 \\ 5 & Guts & 14 \\ 6 & Guts & 2 \\ 7 & Guts & 10 \\ 8 & Guts & 13 \\ 9 & Guts & 28 \\ 10 & Guts & 10 \\ 11 & General & 3 \\ 12 & Guts & 32 \\ 13 & Theme & 8 \\ 14 & Guts & 19 \\ 15 & Guts & 17 \\ 16 & Guts & 30 \\ 17 & Guts & 20 \\ 18 & Guts & 2 \\ 19 & Guts & 33 \\ 20 & Guts & 3 \\ 21 & Team & 7 \end{tabular}
| 1.6
|
I2.3 Determine the smallest positive integer $\gamma$ such that the equation $\sqrt{x}-\sqrt{\beta \gamma}=4 \sqrt{2}$ has an integer solution in $x$.
|
3
|
$$
\begin{array}{l}
\sqrt{x}-\sqrt{24 \gamma}=4 \sqrt{2} \\
\sqrt{x}=2 \sqrt{6 \gamma}+4 \sqrt{2}
\end{array}
$$
The smallest positive integer $\gamma=3$
| 1.6
|
## Task 1.
If $a_{1}, a_{2}, \ldots, a_{2000}$ is a sequence of 2000 positive real numbers, for how many indices $i \in$ $\{1,2, \ldots, 2000\}$ can the equality
$$
a_{i} a_{i+3}=a_{i} a_{i+1}+a_{i+1} a_{i+2}+a_{i+2} a_{i+3} ?
$$
hold? We consider that $a_{j+2000}=a_{j}$ for $j \in\{1,2,3\}$.
|
999
|
## Solution.
For an index $i$, we say it is good if it satisfies the equality in the problem statement.
Assume there exist two consecutive good indices $i, i+1$. Then we have
$$
\begin{aligned}
a_{i} a_{i+3} & =a_{i} a_{i+1}+a_{i+1} a_{i+2}+a_{i+2} a_{i+3} \\
a_{i+1} a_{i+4} & =a_{i+1} a_{i+2}+a_{i+2} a_{i+3}+a_{i+3} a_{i+4}
\end{aligned}
$$
From the first equality, it follows that $a_{i+1}a_{i+3}$, which is a contradiction. Therefore, there do not exist two consecutive good indices, so the number of good indices is at most 1000.
Furthermore, if index $i$ is good, then $a_{i}>a_{i+2}$. Assume there are 1000 good indices. Then these indices are $i, i+2, i+4, \ldots, i+1998$ for some $i$. However, then we have
$$
a_{i}>a_{i+2}>a_{i+4}>\ldots>a_{i+1998}>a_{i+2000}=a_{i}
$$
which is a contradiction. We conclude that there are at most 999 good indices.
Now we construct an example of a 2000-tuple where the indices $1,3,5, \ldots, 1997$ are good. Let $a_{1}>a_{3}>\ldots>a_{1999}$ be arbitrary positive real numbers, and let $a_{2}$ be any positive real number. Assume we have defined the numbers $a_{2}, a_{4}, \ldots, a_{2 i}$ for some $i \in\{1, \ldots, 999\}$.
We recursively define $a_{2 i+2}$ so that $2 i-1$ is a good index, i.e., $a_{2 i+2}$ is defined as a number such that $a_{2 i-1} a_{2 i+2}=a_{2 i-1} a_{2 i}+a_{2 i} a_{2 i+1}+a_{2 i+1} a_{2 i+2}$, or
$$
a_{2 i+2}=a_{2 i} \cdot \frac{a_{2 i-1}+a_{2 i+1}}{a_{2 i-1}-a_{2 i+1}}
$$
It is easy to see that $a_{2 i+2}$ is a well-defined positive real number, since $a_{2 i-1}>a_{2 i+1}$. Thus, the 2000-tuple $(a_{1}, a_{2}, \ldots, a_{2000})$ defined in this way has 999 good indices.
Note: Of course, it is also possible to explicitly construct a sequence with 999 good indices. For example, the sequence
$$
2^{0}, 3^{0}, 2^{-1}, 3^{1}, 2^{-2}, 3^{2}, \ldots, 2^{-999}, 3^{999}
$$
| 5.5
|
13.1. [7-8.7 (20 points), 9.8 (15 points), 10.8 (20 points)] There is a rotating round table with 16 sectors, on which numbers $0,1,2, \ldots, 7,8,7,6, \ldots, 2,1$ are written in a circle. 16 players are sitting around the table, numbered in order. After each rotation of the table, each player receives as many points as the number written on the sector they end up in after the table stops. It turned out that after 13 rotations of the table, player number 5 scored a total of 72 points, and player number 9 scored a total of 84 points. How many points did player number 1 score?
|
20
|
Answer: 20.
Solution. Players No. 5 and No. 9 together scored $72+84=156=12 \cdot 13$ points. In one spin, they can together score no more than 12 points. Therefore, in each of the 13 spins, they together scored 12 points. Note that the 12 points they score can be one of the sums $8+4, 7+5$, $6+6, 5+7$ or $4+8$, when the sector 8 is in front of one of them or between them, i.e., in front of one of the players with numbers $6, 7, 8$. In each of these five cases, player No. 1 scores respectively $4, 3, 2, 1$ or 0 points. This can be expressed by the formula $x_{1}=\frac{x_{5}-x_{9}}{2}+2$, where $x_{n}$ is the number of points scored by the player with number $n$ in this spin. Then the number of points scored by player No. 1 after 13 spins is $\frac{72-84}{2}+2 \cdot 13=20$.
| 5.75
|
7. (10 points) The last 8 digits of $11 \times 101 \times 1001 \times 10001 \times 1000001 \times 111$ are
|
87654321
|
【Analysis】By applying the commutative and associative laws of multiplication to integrate $11 \times 101 \times 1001 \times 10001 \times 1000001 \times 111$, then organize it into $11111111 \times 111111111111$, we can derive that the last 8 digits of $11 \times 101 \times 1001 \times 10001 \times 1000001 \times 111$ are 87654321; based on this, solve the problem.
【Solution】Solution: $11 \times 101 \times 1001 \times 10001 \times 1000001 \times 111$
$$
\begin{array}{l}
=(11 \times 101) \times 1001 \times 10001 \times 1000001 \times 111 \\
=(1111 \times 10001) \times 1001 \times 1000001 \times 111 \\
=11111111 \times 111111 \times 1000001 \\
=11111111 \times 111111111111 ;
\end{array}
$$
Since $1111 \times 1111=1234321, 1111 \times 111111=123444321$,
$$
111111 \times 111111=12345654321, \quad 111111 \times 11111111=1234566654321,
$$
Therefore: $11111111 \times 111111111111=1234567888887654321$,
So the last 8 digits of $11 \times 101 \times 1001 \times 10001 \times 1000001 \times 111$ are 87654321; Answer: The last 8 digits of $11 \times 101 \times 1001 \times 10001 \times 1000001 \times 111$ are 87654321. The answer is: 87654321.
| 4
|
As shown in the figure, $\triangle A B C$ is an isosceles right triangle, $A B=28 \mathrm{~cm}$. A semicircle is drawn with $B C$ as the diameter, and point $D$ is the midpoint of the semicircle arc. Try to find the area of the shaded part. (Take $\pi=\frac{22}{7}$.)
|
252 \text{ cm}^2
|
Geometry, cleverly finding area, cutting and supplementing.
(Method 1)
Take the midpoint $E$ of $B C$, connect $D E$; connect $B D$;
$S_{\triangle A B D}=A B \times B E \div 2=28 \times 14 \div 2=196$ square centimeters;
$S_{\text {sector } B E D}=\frac{1}{4} \times \pi \times B E^{2}=\frac{1}{4} \times \pi \times 14^{2}=49 \pi$ square centimeters;
$S_{\triangle B E D}=B E \times D E \div 2=14 \times 14 \div 2=98$ square centimeters;
$S_{\text {shape } B D}=S_{\text {sector } B E D}-S_{\triangle B E D}=49 \pi-98$ square centimeters;
$S_{\text {shaded }}=S_{\triangle A B D}+S_{\text {shape } B D}=196+(49 \pi-98)=49 \pi+98=49 \times \frac{22}{7}+98=252$ square centimeters.
(Method 2)
Take the midpoint $E$ of $B C$, connect $D E$; connect $B D$;
Since $\triangle A B C$ and $\triangle B D E$ are both isosceles right triangles;
Therefore, $\angle A C B=\angle D B E=45^{\circ}$;
Therefore, $A C / / B D$;
Therefore, $S_{\triangle A B D}=S_{\triangle C B D}$;
$S_{\text {sector } B E D}=\frac{1}{4} \times \pi \times B E^{2}=\frac{1}{4} \times \pi \times 14^{2}=49 \pi$ square centimeters;
$S_{\triangle C E D}=C E \times D E \div 2=14 \times 14 \div 2=98$ square centimeters;
$S_{\text {shaded }}=S_{\text {sector } B E D}+S_{\triangle C E D}=49 \pi+98=49 \times \frac{22}{7}+98=252$ square centimeters.
| 3
|
14. (12 points) Use 36 solid rectangular prisms of size $3 \times 2 \times 1$ to form a large cube of size $6 \times 6 \times 6$. Among all possible arrangements, the maximum number of small rectangular prisms that can be seen from a point outside the large cube is $\qquad$.
|
\documentclass{article}
\usepackage{amsmath}
\usepackage{amssymb}
\begin{document}
31
\end{document}
|
【Answer】Solution: As shown in the figure,
To see the maximum number from the outside, it is necessary to make the rectangles seen from the outside as "deeply" inside the square as possible, the result is as follows: a total of $6 \times 3+3 \times 4+3 \times 1+1=31$ (pieces). Therefore, the answer is: 31.
| 4
|
11. (3 points) There are 20 points below, with each adjacent pair of points being equidistant. By connecting four points with straight lines, you can form a square. Using this method, you can form $\qquad$ squares.
The text above has been translated into English, preserving the original text's line breaks and format.
|
20
|
【Answer】Solution: The number of squares with a side length of 1 unit is 12;
The number of squares with a side length of 2 units is 6;
The number of squares with a side length of 3 units is 2;
The maximum side length is 3 units, any larger and it would not form a square;
In total, there are squares: $12+6+2=20$ (squares).
Answer: A total of 20 squares can be obtained.
Therefore, the answer is: 20.
| 1
|
## Task B-2.1.
For which values of the real parameter $m$ does the inequality $\left(\frac{x_{1}}{x_{2}}\right)^{2}+\left(\frac{x_{2}}{x_{1}}\right)^{2}<47$ hold if $x_{1}$ and $x_{2}$ are the solutions of the equation $x^{2}-\left(2^{m-1}-5\right) x+1=0$?
|
m \in (2,4)
|
## Solution.
For the solutions of the equation $x^{2}-\left(2^{m-1}-5\right) x+1=0$, we have
$$
x_{1}+x_{2}=2^{m-1}-5 \quad \text{and} \quad x_{1} x_{2}=1
$$
Therefore,
$$
\begin{aligned}
\left(\frac{x_{1}}{x_{2}}\right)^{2}+\left(\frac{x_{2}}{x_{1}}\right)^{2} & =\frac{x_{1}^{4}+x_{2}^{4}}{x_{1}^{2} x_{2}^{2}}=\frac{\left(x_{1}^{2}+x_{2}^{2}\right)^{2}-2 x_{1}^{2} x_{2}^{2}}{x_{1}^{2} x_{2}^{2}} \\
& =\frac{\left(\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}\right)^{2}-2\left(x_{1} x_{2}\right)^{2}}{\left(x_{1} x_{2}\right)^{2}} \\
& =\frac{\left(\left(2^{m-1}-5\right)^{2}-2\right)^{2}-2 \cdot 1^{2}}{1^{2}}=\left(\left(2^{m-1}-5\right)^{2}-2\right)^{2}-2
\end{aligned}
$$
The given condition is equivalent to
$$
\begin{array}{ll}
& \left(\left(2^{m-1}-5\right)^{2}-2\right)^{2}-2<47 \\
\Leftrightarrow & \left(\left(2^{m-1}-5\right)^{2}-2\right)^{2}<49 \\
\Leftrightarrow & \left|\left(2^{m-1}-5\right)^{2}-2\right|<7 \\
\Leftrightarrow & -7<\left(2^{m-1}-5\right)^{2}-2<7 \\
\Leftrightarrow & -5<\left(2^{m-1}-5\right)^{2}<9
\end{array}
$$
The inequality $-5<\left(2^{m-1}-5\right)^{2}$ holds for all real numbers $m$, and the inequality $\left(2^{m-1}-5\right)^{2}<9$ is equivalent to $-3<2^{m-1}-5<3$ or $2<2^{m-1}<8$, from which we get $1<m-1<3$. Finally, the desired values of the parameter $m$ are $m \in (2,4)$.
| 3.33
|
The elements of the sequence $\mathrm{Az}\left(x_{n}\right)$ are positive real numbers, and for every positive integer $n$,
$$
2\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{4}=\left(x_{1}^{5}+x_{2}^{5}+\ldots+x_{n}^{5}\right)+\left(x_{1}^{7}+x_{2}^{7}+\ldots+x_{n}^{7}\right)
$$
Determine the elements of the sequence.
|
x_n = n
|
The elements of the sequence $\left(x_{n}\right)$ are positive real numbers, and for every positive integer $n$,
$$
2\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{4}=\left(x_{1}^{5}+x_{2}^{5}+\ldots+x_{n}^{5}\right)+\left(x_{1}^{7}+x_{2}^{7}+\ldots+x_{n}^{7}\right)
$$
Determine the elements of the sequence.
Solution. We will prove by induction that $x_{n}=n$ for every positive integer $n$. For $n=1$, the equation is:
$$
2 x_{1}^{4}=x_{1}^{5}+x_{1}^{7}
$$
Rearranging and factoring:
$$
x_{1}^{4}\left(x_{1}^{2}+x_{1}+2\right)\left(x_{1}-1\right)=0
$$
The only positive real root of this equation is 1.
Assume that $k>1$, and that we have repeated this assertion for $n=1,2, \ldots,(k-1)$, i.e., that
$$
x_{1}=1, x_{2}=2, \ldots, x_{k-1}=k-1
$$
is the unique positive real solution of the defining equation of the sequence when $n=k-1$. We will show that for $n=k$, (1) has a unique solution: $x_{k}=k$.
Write down the $k$-th and $(k-1)$-th equations, and subtract the latter, using the identity $1+2+\ldots+(k-1)=\frac{k(k-1)}{2}$:
$$
\begin{gathered}
2\left(1+2+\ldots+(k-1)+x_{k}\right)^{4}=\left(1^{5}+2^{5}+\ldots+(k-1)^{5}+x_{k}^{5}\right)+\left(1^{7}+2^{7}+\ldots+(k-1)^{7}+x_{k}^{7}\right) \\
2(1+2+\ldots+(k-1))^{4}=\left(1^{5}+2^{5}+\ldots+(k-1)^{5}\right)+\left(1^{7}+2^{7}+\ldots+(k-1)^{7}\right) \\
2\left(\frac{k(k-1)}{2}+x_{k}\right)^{4}-2\left(\frac{k(k-1)}{2}\right)^{4}=x_{k}^{5}+x_{k}^{7}
\end{gathered}
$$
Perform the exponentiations and rearrange the equation:
$$
x_{k}^{7}+x_{k}^{5}-2 x_{k}^{4}-4 k(k-1) x_{k}^{3}-3 k^{2}(k-1)^{2} x_{k}^{2}-k^{3}(k-1)^{3} x_{k}=0
$$
We can divide by $x_{k}$, since it is positive; rearranging the parentheses:
$$
x_{k}^{6}+x_{k}^{4}-2 x_{k}^{3}-\left(4 k^{2}-4 k\right) x_{k}^{2}-\left(3 k^{4}-6 k^{3}+3 k^{2}\right) x_{k}-\left(k^{6}-3 k^{5}+3 k^{4}-k^{3}\right)=0
$$
It can be verified by substitution that $x_{k}=k$ is a solution. Factor out the $\left(x_{k}-k\right)$ root:
$$
\left(x_{k}-k\right)\left(x_{k}^{5}+k x_{k}^{4}+\left(k^{2}+1\right) x_{k}^{3}+\left(k^{3}+k-2\right) x_{k}^{2}+\left(k^{4}-3 k^{2}+2 k\right) x_{k}+\left(k^{5}-3 k^{4}+3 k^{3}-k^{2}\right)\right)=0
$$
We claim that every coefficient in the second factor is positive. It is sufficient to prove this from the fourth term onwards. Indeed,
$$
\begin{aligned}
& k^{3}+k-2 \geq k^{3}+2-2>0 \\
& k^{4}-3 k^{2}+2 k>k^{4}-4 k^{2}+4=\left(k^{2}-2\right)^{2} \geq 0 \text { and } \\
& k^{5}-3 k^{4}-3 k^{3}-k^{2}=k^{2}(k-1)^{3}>0
\end{aligned}
$$
Therefore, since $x_{k}>0$, the second factor is always positive, and the only positive root of the equation is: $x_{k}=k$.
This completes the proof of our statement.
| 5
|
Alice and the Cheshire Cat play a game. At each step, Alice either (1) gives the cat a penny, which causes the cat to change the number of (magic) beans that Alice has from $n$ to $5n$ or (2) gives the cat a nickel, which causes the cat to give Alice another bean. Alice wins (and the cat disappears) as soon as the number of beans Alice has is greater than 2008 and has last two digits 42. What is the minimum number of cents Alice can spend to win the game, assuming she starts with 0 beans?
|
35
|
Consider the number of beans Alice has in base 5. Note that $2008=31013_{5}, 42=132_{5}$, and $100=400_{5}$. Now, suppose Alice has $d_{k} \cdots d_{2} d_{1}$ beans when she wins; the conditions for winning mean that these digits must satisfy $d_{2} d_{1}=32, d_{k} \cdots d_{3} \geq 310$, and $d_{k} \cdots d_{3}=4i+1$ for some $i$. To gain these $d_{k} \cdots d_{2} d_{1}$ beans, Alice must spend at least $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1$ cents (5 cents to get each bean in the "units digit" and $k-1$ cents to promote all the beans). We now must have $k \geq 5$ because $d_{k} \cdots d_{2} d_{1}>2008$. If $k=5$, then $d_{k} \geq 3$ since $d_{k} \cdots d_{3} \geq 3100$; otherwise, we have $d_{k} \geq 1$. Therefore, if $k=5$, we have $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1 \geq 44>36$; if $k>5$, we have $5\left(d_{1}+d_{2}+\cdots+d_{k}\right)+k-1 \geq 30+k-1 \geq 35$. But we can attain 36 cents by taking $d_{k} \cdots d_{3}=1000$, so this is indeed the minimum.
| 5
|
18. (2 marks) Let $A_{1} A_{2} \cdots A_{2002}$ be a regular 2002-sided polygon. Each vertex $A_{i}$ is associated with a positive integer $a_{i}$ such that the following condition is satisfied: If $j_{1}, j_{2}, \cdots, j_{k}$ are positive integers such that $k<500$ and $A_{j_{1}} A_{j_{2}} \cdots A_{j_{k}}$ is a regular $k$-sided polygon, then the values of $a_{j_{1}}, a_{j_{2}}, \cdots, a_{j_{k}}$ are all different. Find the smallest possible value of $a_{1}+a_{2}+\cdots+a_{2002}$.
(2 分) 設 $A_{1} A_{2} \ldots A_{2002}$ 為正 2002 邊形 0 每一頂點 $A_{i}$ 對應正整數 $a_{i}$ 使下列條件成立:如果 $j_{1}, j_{2}, \cdots, j_{k}$為正整數, $k<500$, 而 $A_{j_{1}} A_{j_{2}} \ldots A_{j_{k}}$ 為正 $k$ 邊形時, 則 $a_{j_{1}}, a_{j_{2}}, \cdots, a_{j_{k}}$ 的值互不相同。求 $a_{1}+a_{2}+\ldots+a_{2002}$的最小可能值。
|
287287
|
18. Since $2002=2 \times 7 \times 11 \times 13$, we can choose certain vertices among the 2002 vertices to form regular 7-, 11-, 13-, $\cdots$ polygons (where the number of sides runs through divisors of 2002 greater than 2 and less than 1001). Since $2002=7 \times 286$, so there are at least 286 different positive integers among the $a_{i}{ }^{\prime} s$. Hence the answer is at least $7 \times(1+2+\cdots+286)=\frac{7 \times 286 \times 287}{2}=287 \times 1001=287287$. Indeed this is possible if we assign the number $\left[\frac{i}{7}\right]+1$ to each $A_{i}$, for $i=1,2, \cdots, 2002$.
| 6.33
|
9.2. For what least natural $n$ do there exist integers $a_{1}, a_{2}, \ldots, a_{n}$ such that the quadratic trinomial
$$
x^{2}-2\left(a_{1}+a_{2}+\ldots+a_{n}\right)^{2} x+\left(a_{1}^{4}+a_{2}^{4}+\ldots+a_{n}^{4}+1\right)
$$
has at least one integer root?
(P. Kozlov)
|
6
|
Answer. For $n=6$.
Solution. For $n=6$, we can set $a_{1}=a_{2}=a_{3}=a_{4}=1$ and $a_{5}=a_{6}=-1$; then the quadratic trinomial from the condition becomes $x^{2}-8 x+7$ and has two integer roots: 1 and 7. It remains to show that this is the smallest possible value of $n$.
Suppose the numbers $a_{1}, a_{2}, \ldots, a_{n}$ satisfy the condition of the problem; then the discriminant of the quadratic trinomial from the condition, divided by 4, must be a perfect square. It is equal to
$$
d=\left(a_{1}+a_{2}+\ldots+a_{n}\right)^{4}-\left(a_{1}^{4}+a_{2}^{4}+\ldots+a_{n}^{4}+1\right)
$$
Then the number $d$ is odd and is a square, so it gives a remainder of 1 when divided by 8.
Rewrite the above equality as
$$
d+1+a_{1}^{4}+a_{2}^{4}+\ldots+a_{n}^{4}=\left(a_{1}+a_{2}+\ldots+a_{n}\right)^{4}
$$
and consider it modulo 8. It is not hard to check that the fourth powers of integers give only remainders 0 and 1 when divided by 8, so the right-hand side of the equality gives a remainder of 0 or 1. The left-hand side, however, is comparable to $1+1+k$, where $k$ is the number of odd numbers among $a_{i}$. Therefore, $n \geqslant k \geqslant 6$.
| 6
|
2. Fifteen numbers are arranged in a circle. The sum of any six consecutive numbers is 50. Petya covered one of the numbers with a card. The two numbers adjacent to the card are 7 and 10. What number is under the card?
|
8
|
Answer: 8.
Solution. Let the number at the $i$-th position be $a_{i}(i=1, \ldots, 15$.) Fix 5 consecutive numbers. The numbers to the left and right of this quintet must match. Therefore, $a_{i}=a_{i+6}$. Let's go in a circle, marking the same numbers:
$$
a_{1}=a_{7}=a_{13}=a_{4}=a_{10}=a_{1} .
$$
Now it is clear that for any $i$, $a_{i}=a_{i+3}$, i.e., the numbers go in the following order:
$$
a, b, c, a, b, c, \ldots, a, b, c
$$
From the condition, it follows that
$$
2(a+b+c)=50
$$
Thus, the sum of any three consecutive numbers is 25. Hence the answer.
Scoring. 12 points for a complete solution.
| 2.2
|
2. (10 points) Five pieces of paper are written with $1$, $2$, $3$, $4$, and $5$, facing up from smallest to largest, stacked in a pile. Now, the 1, 3, and 5 are flipped to their backs, and still placed in their original positions. If the entire stack of paper is split at any one piece of paper into two stacks, and the upper stack is reversed and placed back on the lower stack, or if the entire stack of 5 pieces of paper is reversed, it counts as one "reversal". To transform the above arrangement of five pieces of paper so that they are all facing up, the minimum number of "reversals" required is $\qquad$. (The side with the number is the front)
|
5
|
2. (10 points) Five pieces of paper are written with $1, 2, 3, 4, 5$ respectively, facing upwards from smallest to largest, stacked into one pile. Now, the $1, 3,$ and $5$ are flipped to their backs and placed back in their original positions. If the entire stack is split at any one piece of paper into two stacks, and the upper stack is reversed and placed back on the lower stack, or if the entire stack of 5 pieces of paper is reversed, it counts as one "reversal". To transform the five pieces of paper from the above arrangement to all facing upwards, at least 5 "reversals" are required. (The side with the number is the front side)
【Analysis】First, consider the entire stack of paper as composed of 5 "sub-stacks", which can help determine the change in the number of "sub-stacks" after one reversal, leading to the conclusion.
【Solution】Solution: If we consider the entire stack of paper as being composed of parts that are all in the same direction: "sub-stacks", then the original entire stack of paper consists of 5 sub-stacks.
One "reversal" can only start from one piece of paper, placing the top piece of the upper part next to the top piece of the lower part, with the order in between remaining unchanged. After one reversal, the number of "sub-stacks" can only change in three ways: increase by 1, remain unchanged, or decrease by 1. When the entire stack is reversed, the number of "sub-stacks" does not change.
According to the requirement, to turn the 5 into the front side, there must be one reversal of all 5 pieces of paper, and the sequence of the entire stack remains unchanged. To turn 5 sub-stacks into one sub-stack, at least 4 reversals are required. Therefore, at least 5 reversals are needed.
The following explains that 5 reversals can ensure that all 5 pieces of paper are facing upwards: First, reverse the 1, then reverse 1 and 2 together, then reverse $2, 1, 3$, then reverse $3, 1, 2, 4$, and finally reverse $4, 2, 1, 3, 5$ to make them all face upwards, totaling 5 reversals (this is one of the possible sequences of reversals). Therefore, the answer is: 5.
| 2.25
|
Given two positive integers $n$ and $k$. In the plane, there are $n$ circles ($n \geq 2$) such that each circle intersects every other circle at two points, and all these intersection points are pairwise distinct.
Each intersection point is colored with one of $n$ colors such that each color is used at least once and on each of the circles, the same number $k$ of colors is represented.
Determine all values of $n$ and $k$ for which such a coloring is possible.
|
2 \leq k \leq n \leq 3 \text{ or } 3 \leq k \leq n
|
The answer is: $2 \leq k \leq n \leq 3$ or $3 \leq k \leq n$.
Obviously, $k \leq n$ according to the problem statement, and $k \geq 2$, because for $k=1$ all points would have the same color, while the number $n$ of colors should be $\geq 2$. We number the circles and the colors from 1 to n and denote by $F(i, j)$ the set of colors of the intersection points of circles i and j. $F(i, j)$ contains one or two elements.
Let $k=2$. For $n=2$, $F(1,2)=\{1,2\}$ is an allowed coloring. For $n=3$, $F(1,2)=\{3\}$, $F(2,3)=\{1\}, F(3,1)=\{2\}$ is an example of an allowed coloring. Now let $n \geq 4$. To each of the n circles, we assign the set $\{i, j\}$ of the two colors appearing on it. Each of these sets consists of two elements, and each of the n colors must appear in at least two sets, since each colored point is the intersection of two circles. Therefore, each color appears in exactly two sets. For the circle 1 with the set $\{i, j\}$, there are thus at most two other circles whose color sets contain i or j. Since $n \geq 4$, we always find a circle 2 with the set $\{k, l\}$ and $\{k, l\} \cap\{i, j\}=\{ \}$. The intersection points of circles 1 and 2 are then not allowed to be colored, contradiction!
Now we prove by induction a slightly stronger statement than required: For $n \geq k \geq 3$, there always exists an allowed coloring in which the color i appears on the circle i for all $i=1, \ldots, n$. For the base case, we give an example for $k=n=3$ with $F(1,2)=\{1,2\}$, $F(1,3)=\{1,3\}, F(2,3)=\{2,3\}$ and for $k=3, n>3$ the following example of an allowed coloring with the additional condition:
$F(1,2)=\{1,2\}, F(i, i+1)=\{i\}$ for $1<i<n-1, F(n-1, n)=\{n-2, n-1\}$ and $F(i, j)=\{n\}$ for the remaining pairs $(i, j)$ with $1 \leq i<j \leq n$.
Now assume that the stronger statement is true for some $k \geq 3$, and choose $n \geq k+1$. Since $n-1 \geq k \geq 3$, there exists an allowed coloring with the additional condition for the circles or colors 1,2,..., n-1. Now we color the intersection points of circle n: For each $i=1, \ldots, n-1$, one intersection point of circles i and n is colored with color n. Thus, on each of the circles i with $i=1, \ldots, n-1$, exactly $k+1$ colors appear; among them i and $n$. For $i=1, \ldots, k$, the second intersection point of circles i and n is colored with color i, so that now also on circle $n$ exactly $k+1$ colors lie, namely 1 to $k$ and $n$. All other new intersection points are colored with color n, so that no additional colors appear on any circle. This coloring satisfies all conditions.
| 5
|
[ $\underline{\text { Classical Inequalities (Miscellaneous) })]}$
$$
\sqrt{x_{1}^{2}+\left(1-x_{2}\right)^{2}}+\sqrt{x_{2}^{2}+\left(1-x_{3}\right)^{2}}+\ldots+\sqrt{x_{2 n}^{2}+\left(1-x_{1}\right)^{2}}
$$
|
\frac{n}{\sqrt{2}}
|
According to the inequality between the quadratic mean and the arithmetic mean
$$
\begin{aligned}
& \sqrt{2}\left(\sqrt{x_{1}^{2}+\left(1-x_{2}\right)^{2}}+\sqrt{x_{2}^{2}+\left(1-x_{3}\right)^{2}}+\ldots+\sqrt{x_{n}^{2}+\left(1-x_{1}\right)^{2}}\right) \geq \\
& \geq\left|x_{1}\right|+\left|1-x_{2}\right|+\left|x_{2}\right|+\left|1-x_{3}\right|+\ldots+\left|x_{n}\right|+\left|1-x_{1}\right| \geq x_{1}+1-x_{2}+x_{2}+1-x_{3}+\ldots+x_{n}+1-x_{1}=n
\end{aligned}
$$
Equality is achieved when $x_{1}=x_{2}=\ldots=x_{n}=1 / 2$.
## Answer
$\frac{n}{\sqrt{2}}$.
| 4.33
|
10,11
There is a piece of chain consisting of 150 links, each weighing 1 g. What is the smallest number of links that need to be broken so that from the resulting parts, all weights of 1 g, 2 g, 3 g, ..., 150 g can be formed (a broken link also weighs 1 g)?
|
\text{4}
|
Answer: 4 links. According to the solution of problem 5 for grades $7-8$, for a chain consisting of $n$ links, where $64 \leq n \leq 159$, it is sufficient to unfasten 4 links.
| 4.2
|
$12.23 y=\frac{x}{\ln x}$.
The above text is translated into English, please retain the original text's line breaks and format, and output the translation result directly.
However, since the provided text is already in a mathematical format which is universal and does not require translation, the translation is as follows:
$12.23 y=\frac{x}{\ln x}$.
|
(e, e)
|
12.23 The function is defined for $x>0$ and $x \neq 1$. We have
$$
y^{\prime}=\frac{\ln x - x \cdot \frac{1}{x}}{\ln ^{2} x}=\frac{\ln x - 1}{\ln ^{2} x}
$$
Thus, $y^{\prime}=0$ when $\ln x - 1 = 0$, i.e., when $x=e$. Let's construct a table:
| Interval | $(0,1)$ | $(1, e)$ | $e$ | $(e, \infty)$ |
| :---: | :---: | :---: | :---: | :---: |
| $y^{\prime}$ | - | - | 0 | + |
| $y$ | $\searrow$ | $\searrow$ | $\min$ | $\nearrow$ |
Therefore, the function has a minimum at $x=e$. Let's find the value of the function at $x=e$:
$$
y_{\min }=y(e)=\frac{e}{\ln e}=e
$$
Answer: $(e ; e)$ is the point of minimum.
| 3.5
|
6. A factory produces sets of $n>2$ elephants of different sizes. According to the standard, the difference in mass between adjacent elephants within each set should be the same. The inspector checks the sets one by one using a balance scale without weights. For what smallest $n$ is this possible?
|
$n=5$
|
- Omвem: for $n=5$. Let's number the elephants in ascending order of their size, then it is enough to verify that $C_{1}+C_{4}=C_{2}+C_{3}, C_{1}+C_{5}=C_{2}+C_{4}$ and $C_{2}+$ $C_{5}=C_{3}+C_{4}$. These equalities are equivalent to $C_{4}-C_{3}=C_{2}-C_{1}$, $C_{2}-C_{1}=C_{5}-C_{4}$ and $C_{5}-C_{4}=C_{3}-C_{2}$, that is, all adjacent differences are equal. For $n=4$, it is impossible to check, because the weight sets $10,11,12,13$ and $10,11,13,14$ will give the same result for any weighings.
(A. Shapovalov)
## Third Round
| 5
|
7.214. $9^{x}+6^{x}=2^{2 x+1}$.
Translate the above text into English, keeping the original text's line breaks and format, and output the translation result directly.
7.214. $9^{x}+6^{x}=2^{2 x+1}$.
|
0
|
Solution.
Rewrite the equation as $3^{2 x}+2^{x} \cdot 3^{x}-2 \cdot 2^{2 x}=0$ and divide it by $2^{2 x} \neq 0$. Then $\left(\frac{3}{2}\right)^{2 x}+\left(\frac{3}{2}\right)^{x}-2=0 \Rightarrow\left(\left(\frac{3}{2}\right)^{x}\right)=-2$ (no solutions) or $\left(\left(\frac{3}{2}\right)^{x}\right)_{2}=1 \Rightarrow x=0$.
Answer: 0.
| 3
|
After a fair die with faces numbered 1 to 6 is rolled, the number on the top face is $x$. What is the most likely outcome?
|
x > 2
|
With a fair die that has faces numbered from 1 to 6, the probability of rolling each of 1 to 6 is $\frac{1}{6}$. We calculate the probability for each of the five choices. There are 4 values of $x$ that satisfy $x>2$, so the probability is $\frac{4}{6}=\frac{2}{3}$. There are 2 values of $x$ that satisfy $x=4$ or $x=5$, so the probability is $\frac{2}{6}=\frac{1}{3}$. There are 3 values of $x$ that are even, so the probability is $\frac{3}{6}=\frac{1}{2}$. There are 2 values of $x$ that satisfy $x<3$, so the probability is $\frac{2}{6}=\frac{1}{3}$. There is 1 value of $x$ that satisfies $x=3$, so the probability is $\frac{1}{6}$. Therefore, the most likely of the five choices is that $x$ is greater than 2.
| 1.2
|
25 Two equilateral triangles overlap to form a six-pointed star (as shown in the figure). The first 12 positive integers 1, $2, \cdots, 12$ are to be placed at the 12 nodes of the figure, such that the sum of the four numbers on each straight line is equal.
(1) Find the minimum sum of the numbers placed at the six vertices $a_{1}$, $a_{2}, \cdots, a_{6}$ of the six-pointed star;
(2) Prove that the number of different filling schemes that satisfy the condition is even. (For filling schemes $\pi$ and $T$, if scheme $\pi$ can be rotated or flipped to coincide with scheme $T$, they are considered the same filling scheme)
|
24
|
(1) For any filling method that satisfies the conditions, the number filled at point $a_{i}$ is still denoted as $a_{i}, i=1,2, \cdots, 12$. If the sum of the four numbers on each line is $s$, then from $6 s=2(1+2+\cdots+12)$, we get $s=26$;
In $\triangle a_{1} a_{3} a_{5}$, on the three sides, we have
$$
\begin{array}{l}
\left(a_{1}+a_{8}+a_{9}+a_{3}\right)+\left(a_{3}+a_{10}+a_{11}+a_{5}\right) \\
\quad+\left(a_{5}+a_{12}+a_{7}+a_{1}\right)=3 s ;
\end{array}
$$
In $\triangle a z a_{4} a_{6}$, on the three sides, we have
$$
\begin{array}{l}
\left(a_{2}+a_{9}+a_{10}+a_{4}\right)+\left(a_{4}+a_{11}+a_{12}+a_{6}\right) \\
\quad+\left(a_{6}+a_{7}+a_{8}+a_{2}\right)=3 s .
\end{array}
$$
Subtracting the two equations, we get $a_{1}+a_{3}+a_{5}=a_{2}+a_{4}+a_{6}$.
From this, we know that the sum of the numbers at the vertices of the two triangles is equal. If we denote $m=\left(a_{1}+a_{3}+\right.$ $\left.a_{5}\right)+\left(a_{2}+a_{4}+a_{6}\right)$, then $m$ is an even number.
Because in $1,2, \cdots, 12$, the sum of the smallest six numbers $1+2+\cdots+6=21$ is odd, then $m \geqslant 22$. If $m=22$, since in $1,2, \cdots, 12$, the sum of six numbers that equals 22 is only $1,2,3,4,5,7$, dividing these into two groups with equal sums, there is only one unique division:
$$
\{1,3,7\} \text { and }\{2,4,5\} \text {. }
$$
Now, ignoring the specific numbers on the outer circle, and changing $\{1,3,7\}$ and $\{2,4,5\}$ to $\{$ odd, odd, odd $\}$ and $\{$ even, even, odd $\}$, respectively, then under rotation, the filling method of the six vertices is unique.
Now consider the filling method of the six inner numbers. Using the notation $a \sim b$ to indicate that integers $a, b$ have the same parity, since the sum of the four numbers on each line $s$ is even, then $a_{9} \sim a_{8} \sim a_{7} \sim a_{12}, a_{10} \sim$ $a_{11}$, and in the six inner numbers $6, 8, 9, 10, 11, 12$, there are exactly four even numbers and two odd numbers, so $\left\{a_{10}, a_{11}\right\}=\{9,11\}$. Since $a_{10}, a_{11}$ are on one side of the triangle with odd vertices, the sum of the numbers at the two vertices of that side should be $s-(9+11) = 6$, but in $\{1,3,7\}$, there are no two numbers that sum to 6, which is a contradiction. Therefore, $m \neq 22$, and thus the even number $m \geqslant 24$.
When $m=24$, we can actually provide a filling method that meets the requirements (as shown in the figure), so the minimum value sought is 24.
(2) For any filling method $\pi$ that satisfies the conditions, let the numbers at each point be $a_{1}, a_{2}, \cdots, a_{12}$, and let
$$
b_{i}=13-a_{i}, i=1,2, \cdots, 12,
$$
then when $a_{i} \in\{1,2, \cdots, 12\}$, $b_{i} \in\{1,2, \cdots, 12\}$. Now, in the filling method $\pi$, replace $a_{1}, a_{2}, \cdots, a_{12}$ with $b_{1}, b_{2}, \cdots, b_{12}$, to get the filling method $T$, then $T$ is also a filling method that satisfies the conditions; obviously
$$
\sum_{i=1}^{6} a_{i}+\sum_{i=1}^{6} b_{i}=\sum_{i=1}^{6}\left(a_{i}+b_{i}\right)=78,
$$
and $\sum_{i=1}^{6} a_{i}, \sum_{i=1}^{6} b_{i}$ are both even numbers, so $\sum_{i=1}^{6} a_{i} \neq 39, \sum_{i=1}^{6} b_{i} \neq 39$.
Let the set of all filling methods that satisfy the conditions be $M$, and divide $M$ into two disjoint subsets: $M=M_{1} \cup M_{2}$, where, in $M_{1}$, each filling method $\pi_{1}=\left(a_{1}, a_{2}, \cdots\right.$, $a_{12}$ ), the sum of the numbers at the six vertices $\sum_{i=1}^{6} a_{i}39$.
Make a correspondence between the filling method $\pi_{1}=\left(a_{1}, a_{2}, \cdots, a_{12}\right)$ in $M_{1}$ and the filling method $\pi_{2}=$ $\left(b_{1}, b_{2}, \cdots, b_{12}\right)$ in $M_{2}$, such that $b_{i}=13-a_{i}, i=1,2, \cdots, 12$, this correspondence is one-to-one, therefore, $\left|M_{1}\right|=\left|M_{2}\right|, M_{1} \cap M_{2}=\varnothing$, and $|M|=$ $\left|M_{1} \cup M_{2}\right|=2\left|M_{1}\right|$, i.e., the number of elements in $M$ is even. That is, the number of different filling methods that satisfy the conditions is even.
| 5.2
|
2. The coordinates $(x ; y)$ of points in the square $\{(x ; y):-\pi \leq x \leq \pi, 0 \leq y \leq 2 \pi\}$ satisfy the system of equations $\left\{\begin{array}{c}\sin x+\sin y=\sin 2 \\ \cos x+\cos y=\cos 2\end{array}\right.$. How many such points are there in the square? Find the coordinates $(x ; y)$ of the point with the smallest ordinate.
|
\left(2+\frac{\pi}{3}, 2-\frac{\pi}{3}\right)
|
Answer: 1) two points
$$
\text { 2) } x=2+\frac{\pi}{3}, y=2-\frac{\pi}{3}
$$
| 2.25
|
9. Let $a+b=1, b>0, a \neq 0$, then the minimum value of $\frac{1}{|a|}+\frac{2|a|}{b}$ is
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
2 \sqrt{2}-1
|
Solve $2 \sqrt{2}-1$.
Analysis $\frac{1}{|a|}+\frac{2|a|}{b}=\frac{a+b}{|a|}+\frac{2|a|}{b}=\frac{a}{|a|}+\left(\frac{b}{|a|}+\frac{2|a|}{b}\right) \geq \frac{a}{|a|}+2 \sqrt{\frac{b}{|a|} \cdot \frac{2|a|}{b}}=2 \sqrt{2}+\frac{a}{|a|}$, where the equality holds when $\frac{b}{|a|}=\frac{2|a|}{b}$, i.e., $b^{2}=2 a^{2}$.
When $a>0$, $\frac{1}{|a|}+\frac{2|a|}{b} \geq 2 \sqrt{2}+1$, the minimum value is reached when $a=\sqrt{2}-1, b=\sqrt{2} a=2-\sqrt{2}$; when $a<0$, $\frac{1}{|a|}+\frac{2|a|}{b} \geq 2 \sqrt{2}-1$, the minimum value $2 \sqrt{2}-1$ is reached when $a=-(\sqrt{2}+1), b=-\sqrt{2} a$.
| 9
|
25. A scout is in a house with four windows arranged in a rectangular shape. He needs to signal to the sea at night by lighting a window or several windows. How many different signals can he send?
|
10
|
25. Let's schematically represent the windows and measure them:
a) Lighting all four windows gives one signal;
b) Lighting one of the windows is perceived as one signal, as in the dark, the position of the windows relative to the house cannot be distinguished;
c) Lighting two windows can give 4 different signals: one signal by lighting windows 1,4 or 2,3; one signal by lighting windows 1,2 or 4,3; two signals by lighting windows 1,3 and 2,4, i.e., we have the following configurations:
1)
2) $\bullet \cdot 3)$
- 4)
d) Lighting three windows can give four signals: $1,2,3$; $2,3,4$; $3,4,1$ and $4,1,2$, i.e., we have the following configurations:
1)
2)
3)
4)
In total, we have different signals: $1+1+4+4=10$.
| 1.6
|
6.014. $\frac{4}{x^{2}+4}+\frac{5}{x^{2}+5}=2$.
|
$x=0$
|
## Solution.
Domain: $x \in R$.
$\frac{2 x^{4}+9 x^{2}}{\left(x^{2}+4\right)\left(x^{2}+5\right)}=0 \Leftrightarrow 2 x^{4}+9 x^{2}=0 \Leftrightarrow x^{2}\left(2 x^{2}+9\right)=0$,
$x^{2}=0, x_{1}=0$ or $2 x^{2}+9=0, x_{2,3} \in \varnothing$.
Answer: $x=0$.
| 2
|
6. Find the greatest possible value of $\gcd(x+2015 y, y+2015 x)$, given that $x$ and $y$ are coprime numbers.
|
4060224
|
Answer: $2015^{2}-1=4060224$. Solution. Note that the common divisor will also divide $(x+2015 y)-2015(y+2015 x)=\left(1-2015^{2}\right) x$. Similarly, it divides $\left(1-2015^{2}\right) y$, and since $(x, y)=1$, it divides $\left(1-2015^{2}\right)$. On the other hand, if we take $x=1, y=2015^{2}-2016$, then we get $\gcd(x+2015 y, y+2015 x)=2015^{2}-1$.
| 8
|
3. Given $n^{2}$ points arranged in the plane in the form of a square grid $n \times n$. A broken line of length $l$ is the union of closed segments $A_{0} A_{1}$, $A_{1} A_{2}$, $A_{2} A_{3}, \ldots, A_{l-1} A_{l}$ in that plane. Determine the smallest natural number $l$ for which there exists a broken line of length $l$ on which all $n^{2}$ observed points lie.
|
$2n-2$
|
3. Let the desired value of the number $l$ be denoted by $l_{n}$. Trivially, $l_{1}=1$ and $l_{2}=3$. The examples in the figure show that $l_{3} \leqslant 4$ and, in general, $l_{n} \leqslant 2 n-2$ for $n \geqslant 3$.
Assume that the broken line $\mathcal{C}$ of length $l$ covers all $n^{2}$ points. Let there be $a$ horizontal and $b$ vertical segments among the segments of the line $\mathcal{C}$. The remaining $l-a-b$ segments of the line $\mathcal{C}$
are bent by horizontal and vertical
segments to form a rectangular grid $S$ of dimensions $(n-a) \times(n-b)$.
- If $a \geqslant n$ (analogously for $b \geqslant n$), there is no grid $S$, but at least $n-1$ segments are needed to connect $n$ horizontal segments, so $l \geqslant 2 n-1$.
- If $a=n-1$ (analogously for $b=n-1$), the grid $S$ consists of $n-b$ points, and each diagonal segment covers at most one, so we need at least $n-b$ more segments, which gives a total of $l \geqslant(n-1)+b+(n-b)=2 n-1$ segments.
- If $a<n-2$ and $b<n-2$, the convex hull of the grid $S$ consists of $2(2 n-a-b-2)$ points, and each diagonal segment covers at most two, so we need at least $2 n-a-b-2$ more segments. Thus, in total, we have $l \geqslant a+b+(2 n-a-b-2)=2 n-2$ segments.
Therefore, $l_{n}=2 n-2$ for all $n \geqslant 3$.
| 3.4
|
2. Find all positive integers $n$ $(n \geqslant 3)$ such that there exists a set $M$ with $n$ elements, where the elements are distinct non-zero vectors of equal length, and the following conditions are satisfied: $\sum_{u \in M} u=0$, and for any $v, w \in M$, $\boldsymbol{v}+\boldsymbol{w} \neq \mathbf{0}$.
|
\{n \in \mathbf{N} \mid n \geqslant 3, n \neq 4\}
|
2. First, for any odd number $n$ not less than 3, take $M$ as the $n$ distinct complex roots of the equation $z^{n}-1=0$. Clearly, the set $M$ satisfies the requirements.
Next, consider even numbers $n$ not less than 6.
Let $\frac{n}{2}=k$, first consider the decomposition of $\frac{1}{2}$.
From $\frac{1}{n}=\frac{1}{n+1}+\frac{1}{n(n+1)}$, we know that $\frac{1}{2}$ can be decomposed into the sum of $k-1$ distinct unit fractions.
Assume $\frac{1}{2}=a_{1}+a_{2}+\cdots+a_{k-1}$, first take $k$ unit vectors above the $x$-axis, whose x-coordinates are sequentially $\frac{1}{2},-a_{1}, \cdots,-a_{n}$, then reflect these vectors about the $x$-axis to get $n$ vectors. Let this set of $n$ vectors be $M$, clearly the set $M$ satisfies the conditions.
Finally, prove that $n=4$ does not satisfy the conditions.
Assume the four vectors are $(1,0),\left(x_{1}, y_{1}\right)$, $\left(x_{2}, y_{2}\right),\left(x_{3}, y_{3}\right)$. To satisfy the conditions, we need $y_{i} \neq 0$ $(i=1,2,3)$.
Assume $y_{1}>0, y_{2}>0, y_{3}<0$. At this point,
$$
\begin{array}{l}
x_{1}+x_{2}+x_{3}=-1, \\
y_{1}+y_{2}+y_{3}=0, \\
x_{i}^{2}+y_{i}^{2}=1(i=1,2,3) . \\
\text { Then }\left\{\begin{array}{l}
\sqrt{1-x_{1}^{2}}+\sqrt{1-x_{2}^{2}}=-y_{3}, \\
x_{1}+x_{2}=-1-x_{3} .
\end{array}\right. \\
(1)^{2}+(2)^{2} \text { gives } \\
x_{1} x_{2}+\sqrt{1-x_{1}^{2}-x_{2}^{2}+x_{1}^{2} x_{2}^{2}}=x_{3} . \\
\text { Let }\left\{\begin{array}{l}
x_{1}+x_{2}=a, \\
x_{1} x_{2}=b .
\end{array}\right.
\end{array}
$$
Substituting into equation (3) gives
$$
\begin{array}{l}
b+\sqrt{1-a^{2}+2 b+b^{2}}=-a-1 \\
\Rightarrow a(a+b+1)=0 .
\end{array}
$$
If $a=0$, then $x_{3}=-1$, at this time, $y_{3}=0$, which is a contradiction.
If $a+b+1=0$, it can be deduced that
$$
\left(x_{1}+1\right)\left(x_{2}+1\right)=0 \text {, }
$$
At this time, $y_{1}$ or $y_{2}$ must be 0, which is a contradiction.
In summary, the solution is $\{n \in \mathbf{N} \mid n \geqslant 3, n \neq 4\}$.
| 3
|
Isosceles $\triangle ABC$ has equal side lengths $AB$ and $BC$. In the figure below, segments are drawn parallel to $\overline{AC}$ so that the shaded portions of $\triangle ABC$ have the same area. The heights of the two unshaded portions are 11 and 5 units, respectively. What is the height of $h$ of $\triangle ABC$?
$\textbf{(A) } 14.6 \qquad \textbf{(B) } 14.8 \qquad \textbf{(C) } 15 \qquad \textbf{(D) } 15.2 \qquad \textbf{(E) } 15.4$
|
14.6
|
First, we notice that the smaller isosceles triangles are similar to the larger isosceles triangles. We can find that the area of the gray area in the first triangle is $[ABC]\cdot\left(1-\left(\tfrac{11}{h}\right)^2\right)$. Similarly, we can find that the area of the gray part in the second triangle is $[ABC]\cdot\left(\tfrac{h-5}{h}\right)^2$. These areas are equal, so $1-\left(\frac{11}{h}\right)^2=\left(\frac{h-5}{h}\right)^2$. Simplifying yields $10h=146$ so $h=\boxed{\textbf{(A) }14.6}$.
~MathFun1000 (~edits apex304)
| 2.75
|
12. Given that $m, n, t (m<n)$ are all positive integers, points $A(-m, 0), B(n, 0), C(0, t)$, and $O$ is the origin. Suppose $\angle A C B=90^{\circ}$, and
$$
O A^{2}+O B^{2}+O C^{2}=13(O A+O B-O C) \text {. }
$$
(1) Find the value of $m+n+t$;
(2) If the graph of a quadratic function passes through points $A, B, C$, find the expression of this quadratic function.
|
$y = -\frac{1}{3} x^{2} + \frac{8}{3} x + 3$
|
12. (1) According to the problem, we have
$$
O A=m, O B=n, O C=t \text {. }
$$
From $\angle A C B=90^{\circ}, O C \perp A B$, we get
$$
O A \cdot O B=O C^{2} \Rightarrow m n=t^{2} \text {. }
$$
From the given equation, we have
$$
\begin{array}{l}
m^{2}+n^{2}+t^{2}=13(m+n-t) . \\
\text { Also, } m^{2}+n^{2}+t^{2} \\
=(m+n+t)^{2}-2(m n+n t+t m) \\
=(m+n+t)(m+n-t),
\end{array}
$$
$$
\text { Therefore, }(m+n+t)(m+n-t)=13(m+n-t) \text {. }
$$
From the given, $m+n-t \neq 0$, thus,
$$
m+n+t=13 \text {. }
$$
(2) From $m n=t^{2}, m+n=13-t(m0 \\
\Rightarrow(3 t-13)(t+13)<0 \\
\Rightarrow-13<t<\frac{13}{3} .
\end{array}
$$
Since $t$ is a positive integer, we have $t=1,2,3,4$.
When $t=1,2,4$, we get the equations respectively
$$
\begin{array}{l}
x^{2}-12 x+1=0, \\
x^{2}-11 x+4=0, \\
x^{2}-9 x+16=0,
\end{array}
$$
None of the above equations have integer solutions;
When $t=3$, we get the equation
$$
x_{1}^{2}-10 x+9=0 \text {, }
$$
Solving it, we get $m=1, n=9$.
Thus, $t=3, m=1, n=9$.
Therefore, the points are $A(-1,0), B(9,0), C(0,3)$.
Assume the quadratic function is
$$
y=a(x+1)(x-9) \text {. }
$$
Substituting the coordinates of point $C(0,3)$ into the above equation, we get
$$
a=-\frac{1}{3} \text {. }
$$
Hence, $y=-\frac{1}{3}(x+1)(x-9)$
$$
\Rightarrow y=-\frac{1}{3} x^{2}+\frac{8}{3} x+3 \text {. }
$$
| 3
|
497. Shuffling Cards. An elementary method of shuffling cards consists of taking a deck face down in the left hand and transferring the cards one by one to the right hand; each successive card is placed on top of the previous one: the second on top of the first, the fourth on top of the third, and so on until all the cards have been transferred. If you repeat this procedure several times with any even number of cards, you will find that after a certain number of repeated shuffles, the cards will return to their original order. If you have \(2,4,8,16,32,64\) cards, it will take \(2,3,4,5\), 6,7 shuffles respectively for the cards to return to their original order.
\footnotetext{
* The correct order is: Ace, Two, Three, Four, Five, Six, Seven, Eight, Nine, Ten, Jack, Queen, King.
}
How many times do you need to shuffle a deck of 14 cards?
|
14
|
497. To shuffle 14 cards in the manner described above and return them to their original order, it takes 14 shuffles, although in the case of 16 cards, only 5 are required. We cannot delve into the nature of this phenomenon here, but the reader may find it interesting to conduct an independent investigation of this question.
[For the mathematical theory of such shuffling, see W. W. Rouse Ball, “Mathematical Recreations and Essays” (N. Y., 1960, pp. 310-311). This shuffling is sometimes called “Monge’s shuffle,” after the famous 18th-century French mathematician Gaspard Monge, who first invented it. M. G.]
| 4
|
5. The number of real roots of the equation $\frac{\left(x^{2}-x+1\right)^{3}}{x^{2}(x-1)^{2}}=\frac{\left(\pi^{2}-\pi+1\right)^{3}}{\pi^{2}(\pi-1)^{2}}$ with respect to $x$ is exactly $($ )
A. 1
B. 2
C. 4
D. 6
|
6
|
5. D
From the given conditions, it is clear that $x=\pi$ is a root of the original equation. Let's denote the left side as $f(x)$. It is easy to verify:
$$
f\left(\frac{1}{x}\right)=f(x), f(1-x)=f(x), f\left(\frac{1}{1-x}\right)=f(x), f\left(1-\frac{1}{x}\right)=f
$$
$(x), f\left(\frac{x}{x-1}\right)=f(x)$. Therefore, the original equation has exactly 6 distinct real roots: $\pi, \frac{1}{\pi}, 1-\pi$,
$$
\frac{1}{1-\pi}, 1-\frac{1}{\pi}, \frac{\pi}{\pi-1} .
$$
| 5
|
7. From the sides and diagonals of a regular 12-sided polygon, three different segments are randomly selected. The probability that their lengths are the side lengths of a triangle is $\qquad$
|
\frac{223}{286}
|
7. $\frac{223}{286}$.
Let the diameter of the circumscribed circle of a regular 12-sided polygon be 1. Then, the lengths of all $\mathrm{C}_{12}^{2}=66$ line segments fall into 6 categories, which are
$$
\begin{array}{l}
d_{1}=\sin 15^{\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}, \\
d_{2}=\sin 30^{\circ}=\frac{1}{2}, \\
d_{3}=\sin 45^{\circ}=\frac{\sqrt{2}}{2} \text { (please note) } \\
d_{4}=\sin 60^{\circ}=\frac{\sqrt{3}}{2}, \\
d_{5}=\sin 75^{\circ}=\frac{\sqrt{6}+\sqrt{2}}{4}, \\
d_{6}=1,
\end{array}
$$
Among them, $d_{1}, d_{2}, \cdots, d_{5}$ each have 12 segments, and $d_{6}$ has 6 segments.
Clearly, the combinations that cannot form a triangle are of the following four types:
$(2,2,6)$ type, with $\mathrm{C}_{12}^{2} \mathrm{C}_{6}^{1}$ ways;
$(1,1, k)(k \geqslant 3)$ type, with $\mathrm{C}_{12}^{2} \mathrm{C}_{42}^{1}$ ways;
$(1,2, k)(k \geqslant 4)$ type, with $\mathrm{C}_{12}^{1} \mathrm{C}_{12}^{1} \mathrm{C}_{30}^{2}$ ways;
$(1,3, k)(k \geqslant 5)$ type, with $\mathrm{C}_{12}^{1} \mathrm{C}_{12}^{1} \mathrm{C}_{30}^{2}$ ways.
Therefore, the required probability is $1-\frac{63}{286}=\frac{223}{286}$.
| 7
|
Riley has 64 cubes with dimensions $1 \times 1 \times 1$. Each cube has its six faces labelled with a 2 on two opposite faces and a 1 on each of its other four faces. The 64 cubes are arranged to build a $4 \times 4 \times 4$ cube. Riley determines the total of the numbers on the outside of the $4 \times 4 \times 4$ cube. How many different possibilities are there for this total?
|
49
|
We can categorize the 64 small cubes into four groups: 8 cubes that are completely in the interior of the larger cube (and are completely invisible), $4 \times 6=24$ "face cubes" that have exactly one of their faces showing, $2 \times 12=24$ "edge cubes" that have exactly two faces showing, and 8 "corner cubes" that have 3 faces showing.
Notice that $8+24+24+8=64$, so this indeed accounts for all 64 small cubes.
The diagram below has all visible faces of the smaller cubes labelled so that faces of edge cubes are labelled with an $\mathbf{E}$, faces of face cubes are labelled with an $\mathbf{F}$, and faces of corner cubes are labelled with a $\mathbf{C}$ :
Each of the 8 corner cubes has 3 of its faces exposed.
Because of the way the faces are labelled on the small cubes, each of the 8 corner cubes will always contribute a total of $1+1+2=4$ to the sum of the numbers on the outside.
Regardless of how the small cubes are arranged, the corner cubes contribute a total of $8 \times 4=32$ to the total of all numbers on the outside of the larger cube.
The edge cubes can each show either a 1 and a 1 or a 1 and a 2 , for a total of either 2 or 3 .
Thus, each edge cube contributes a total of either 2 or 3 to the total on the outside of the larger cube.
This means the smallest possible total that the edge cubes contribute is $24 \times 2=48$, and the largest possible total that they contribute is $24 \times 3=72$.
Notice that it is possible to arrange the edge cubes to show any total from 48 to 72 inclusive.
This is because if we want the total to be $48+k$ where $k$ is any integer from 0 to 24 inclusive, we simply need to arrange exactly $k$ of the edge cubes to show a total of 3 .
Each of the face cubes shows a total of 1 or a total of 2 . There are 24 of them, so the total showing on the face cubes is at least 24 and at most $24 \times 2=48$.
Similar to the reasoning for the edge cubes, every integer from 24 to 48 inclusive is a possibility for the total showing on the face cubes.
Therefore, the smallest possible total is $32+48+24=104$, and the largest possible total is $32+72+48=152$.
By earlier reasoning, every integer between 104 and 152 inclusive is a possibility, so the number of possibilities is $152-103=49$.
ANSWER: 49
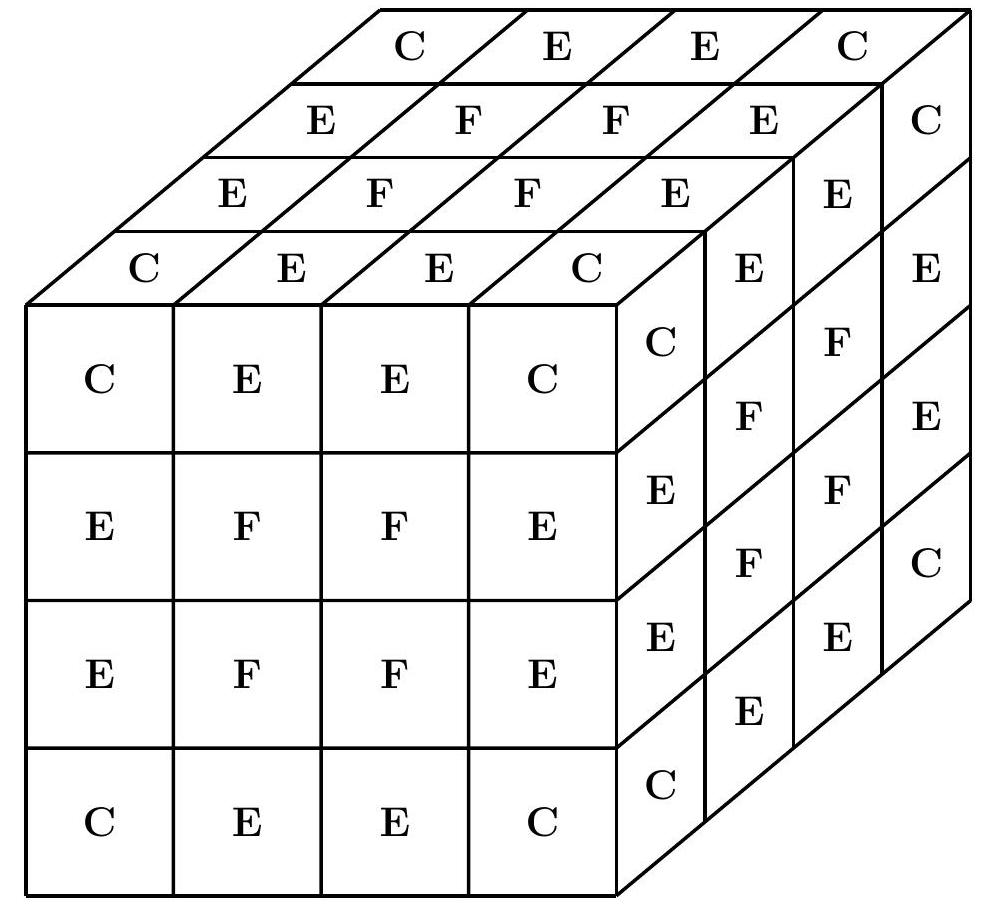
| 4
|
16. Given the six-digit number $\overline{9786 \square}$ is a multiple of $\mathbf{99}$, the quotient when this six-digit number is divided by $\mathbf{99}$ is ( ).
|
6039
|
$\begin{array}{l}\text { [Analysis] Let } 99 \mid \overline{A 9786 B} \text {, sum of pairs from right to left } \\ 99 \mid \overline{A 9}+78+\overline{6 B} \text {, i.e., } 99|78+69+\overline{A B} \Rightarrow 99| 48+\overline{A B} \\ \overline{A B}=51 \text {, i.e., } \mathrm{A}=5, \mathrm{~B}=1 \\ 597861 \div 99=6039\end{array}$
| 1.5
|
The base of the right prism $A B C A_{1} B_{1} C_{1}$ is an isosceles triangle $A B C$, where $A B=B C=5$, $\angle A B C=2 \arcsin 3 / 5$. A plane perpendicular to the line $A_{1} C$ intersects the edges $A C$ and $A_{1} C_{1}$ at points $D$ and $E$ respectively, such that $A D=1 / 3 A C, E C_{1}=1 / 3 A_{1} C_{1}$. Find the area of the section of the prism by this plane.
|
\frac{40}{3}
|
Let $M$ be the midpoint of the base $AC$ of the isosceles triangle $ABC$ (Fig. 1). From the right triangle $AMB$ we find that
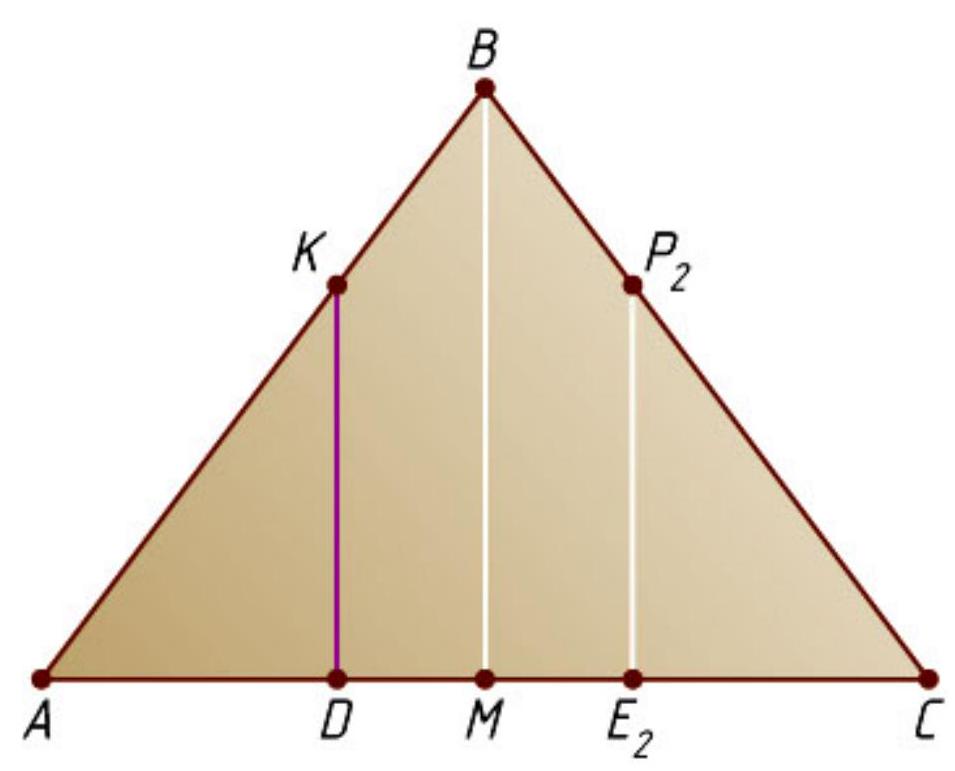
Fig. 1
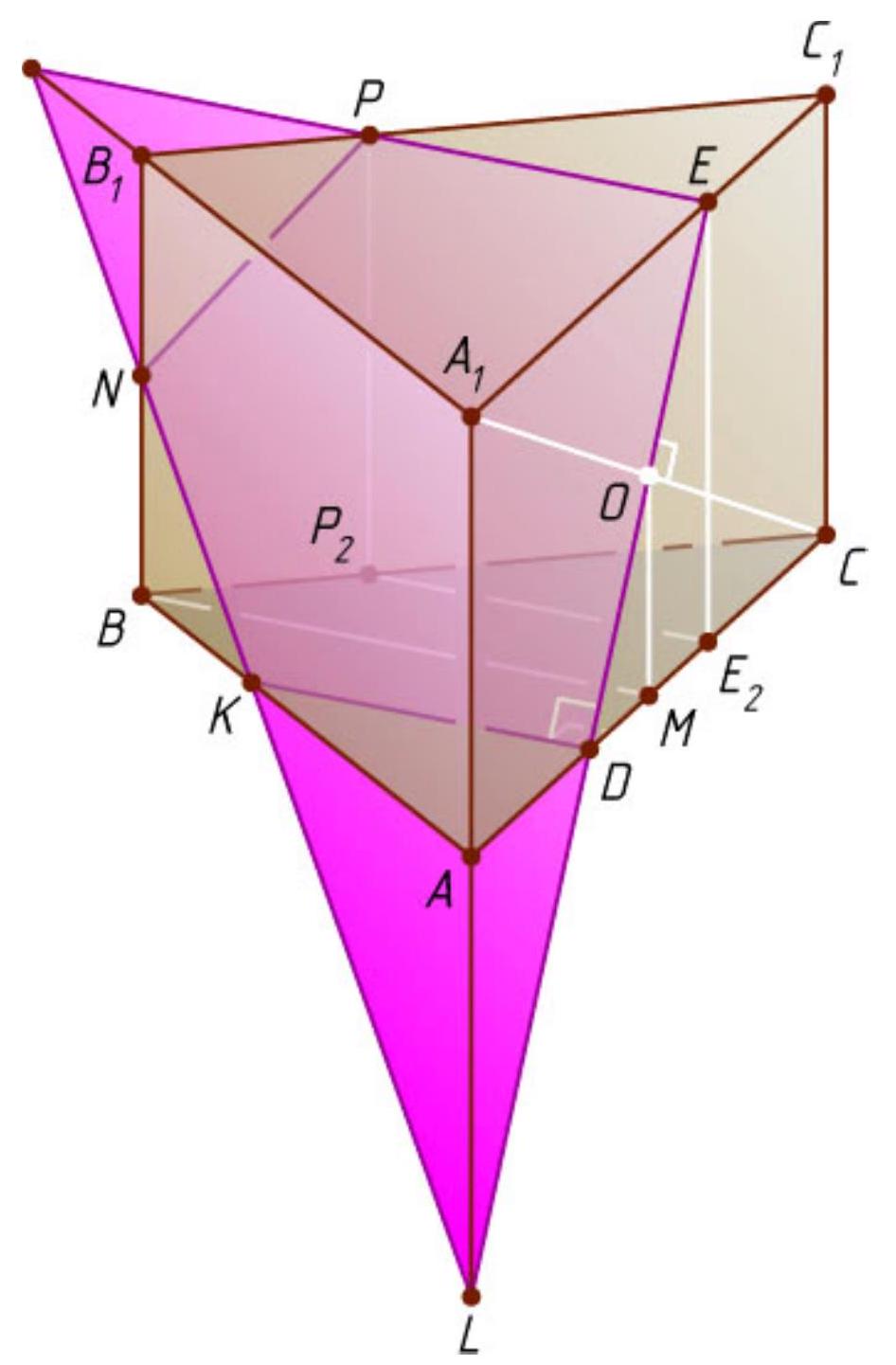
Fig. 2
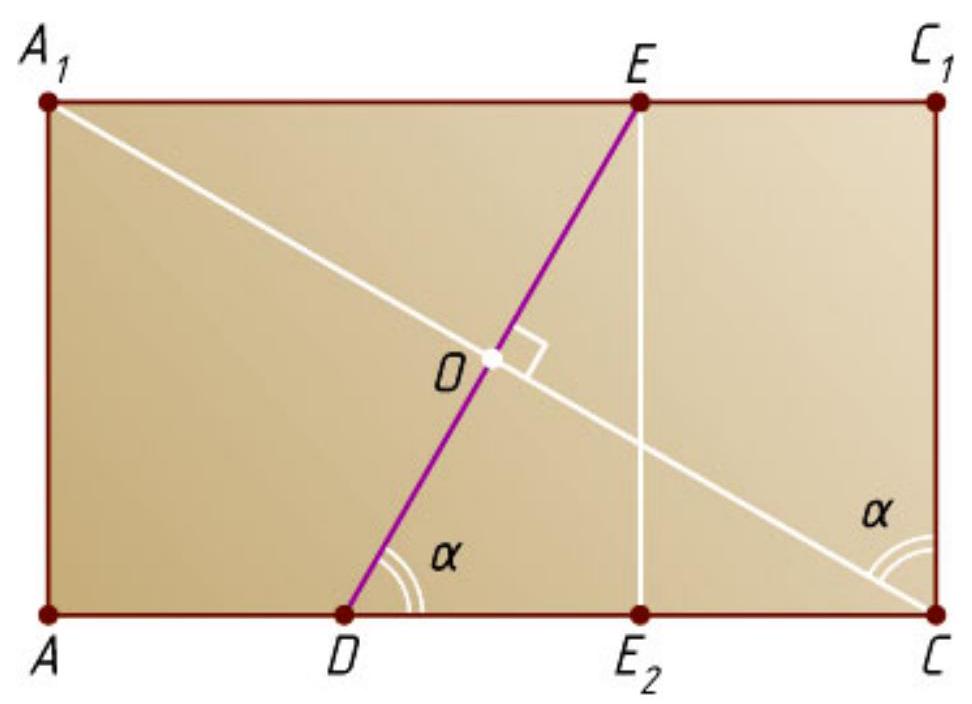
Fig. 3
$AM = AB \sin \angle ABM = 5 \cdot \begin{aligned} & 3 \\ & 5\end{aligned} = 3, \quad BM = \sqrt{AB^2 - AM^2} = \sqrt{25 - 9} = 4$.
Then
$AC = 2AM = 6, \quad AD = \frac{1}{3}AC = 2, \quad C_1E = \frac{1}{3}A_1C_1 = 2$.
Since the line $A_1C$ is perpendicular to the cutting plane (Fig. 2), then $A_1C \perp DE$. Let $O$ be the intersection point of segments $A_1C$ and $DE$. From the equality of right triangles $A_1OE$ and $COD$ (by hypotenuse and acute angle), it follows that $O$ is the midpoint of $A_1C$. Therefore, the perpendicular dropped from point $O$ to $AC$ passes through point $M$, and since the prism is straight, this perpendicular lies in the plane of the face $AA_1C_1C$.
Let $K$ be the intersection point of the cutting plane with the line $AB$. The line $A_1C$ is perpendicular to the cutting plane containing the line $DK$, so $A_1C \perp DK$. By the theorem of three perpendiculars, $DK \perp AC$, since $AC$ is the orthogonal projection of the inclined line $A_1C$ onto the plane $ABC$. Triangles
$ADK$ and $AMB$ are similar with a coefficient $k = \frac{AD}{AM} = \frac{2}{3}$, so
$AK = k \cdot AB = \frac{2}{3} AB < AB$.
Thus, point $K$ lies on the segment $AB$. Similarly, point $P$ of the intersection of the plane with the line $B_1C_1$ lies on the edge $B_1C_1$. In this case, $EP \parallel DK$ and $EP = DK$.
Let the lines $ED$ and $AA_1$ intersect at point $L$, and the lines $LK$ and $BB_1$ intersect at point $N$. Then the section of the prism in question is the pentagon $DKNPE$. Its orthogonal projection onto the plane $ABC$ is the pentagon $DKBP_2E_2$ (Fig. 1, 2), where $P_2$ and $E_2$ are the orthogonal projections of points $P$ and $E$ onto the plane $ABC$. Then
$S_{\triangle CE_2P_2} = S_{\triangle ADK} = k^2 \cdot S_{\triangle AMB} = k^2 \cdot \frac{1}{2} \cdot AM \cdot BM = \left(\frac{2}{3}\right)^2 \cdot \frac{1}{2} \cdot 3 \cdot 4 = \frac{8}{3}$,
$S_{DKBP_2E_2} = S_{\triangle ABC} - 2S_{\triangle ADK} = \frac{1}{2} \cdot AC \cdot BM - 2S_{\triangle ADK} = \frac{1}{2} \cdot 6 \cdot 4 - 2 \cdot \frac{8}{3} = \frac{20}{3}$.
Let $h$ be the height (lateral edge) of the prism. Consider the face $AA_1C_1C$ (Fig. 3). Denote $\angle A_1CC_1 = \angle EE_2D = \alpha$. From the right triangles $CA_1C_1$ and $DEE_2$ we find that
$\tan \alpha = \frac{A_1C_1}{CC_1} = \frac{6}{h}$ and $\tan \alpha = \frac{EE_2}{DE_2} = \frac{h}{2}$,
from which $h = 2\sqrt{3}$ and $\tan \alpha = \sqrt{3}$. Therefore, $\alpha = 60^\circ$.
Since $CD \perp KD$ and $ED \perp KD$, the angle $EDC$ is the linear angle of the dihedral angle between the cutting plane and the plane $ABC$, and since $\angle EDC = \alpha = 60^\circ$, then, by the theorem of the area of the orthogonal projection of a polygon,
$S_{DKNPE} = \frac{S_{DKBP_2E_2}}{\cos \alpha} = \frac{\frac{20}{3}}{\frac{1}{2}} = \frac{40}{3}$.
| 4.2
|
10. Real numbers $x, y$ satisfy $x^{2}+y^{2}=20$, then the maximum value of $x y+8 x+y$ is
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
42
|
Rong Ge 42.
Analysis Note $x y \leq \frac{1}{4} x^{2}+y^{2}, 8 x \leq x^{2}+16, y \leq \frac{1}{4} y^{2}+1$, adding these three inequalities yields
$$
x y+8 x+y \leq \frac{5}{4}\left(x^{2}+y^{2}\right)+17=42
$$
and when $x=4, y=2$, the equality can be achieved, so the maximum value of $x y+8 x+y$ is 42.
Alternatively, the Cauchy inequality can be used directly
$$
(x y+8 x+y)^{2} \leq\left(x^{2}+8^{2}+y^{2}\right)\left(y^{2}+x^{2}+1^{2}\right)=84 \cdot 21=42^{2}
$$
yielding the maximum value of 42.
| 5
|
a) We have 3 initially empty urns. One of them is chosen at random with equal probability (1/3 for each). Then, a ball is placed inside the chosen urn. The process is repeated until one of the urns has two balls. What is the probability that when the process ends, the total number of balls in all urns is equal to 2?
b) Now we have 2014 initially empty urns. Repeating the same process as before, what is the probability that at the end there will be exactly 10 balls in the urns?
|
\frac{2013}{2014} \cdot \frac{2012}{2014} \cdot \frac{2011}{2014} \cdot \frac{2010}{2014} \cdot \frac{2009}{2014} \cdot \frac{2008}{2014} \cdot \frac{2007}{2014} \cdot \frac{2006}{2014} \cdot \frac{9}{2014}
|
Solution
a) First, a ball is placed in some urn. For the process to end with two balls, it is necessary that, in the next step, the next ball is placed in the same urn where the first ball was placed. This has a probability of 1/3. Therefore, the probability that the process ends with two balls is equal to $1 / 3$.
b) First, a ball is placed in some urn. In the next step, it is necessary that the next ball be placed in a different urn from the first one chosen. Otherwise, the process ends! Since there are 2013 empty urns (one is already occupied), the probability of this happening is
$$
\frac{2013}{2014}
$$
In the third step, a new urn is chosen. For the process not to end, it is necessary that this new urn chosen is different from the previous two. The probability of this happening is
$$
\frac{2012}{2014}
$$
In the fourth step, a new urn is chosen. By the same argument as before, the probability that the chosen urn is different from the previous ones is
$$
\frac{2011}{2014}
$$
and so on until the ninth urn, whose probability will be
$$
\frac{2006}{2014}
$$
For the process to end with ten balls, it is necessary that the tenth ball be placed in an urn that already has a ball! Since we have, up to this point, nine occupied urns and there are 2014 urns, the probability of this occurring is
$$
\frac{9}{2014}
$$
Thus, the probability that the process ends with 10 balls is equal to the product of the probabilities described above, which gives us
$$
\frac{2013}{2014} \cdot \frac{2012}{2014} \cdot \frac{2011}{2014} \cdot \frac{2010}{2014} \cdot \frac{2009}{2014} \cdot \frac{2008}{2014} \cdot \frac{2007}{2014} \cdot \frac{2006}{2014} \cdot \frac{9}{2014}
$$
as the result.
| 5.67
|
4. In acute triangle $A B C, M$ and $N$ are the midpoints of sides $A B$ and $B C$, respectively. The tangents to the circumcircle of triangle $B M N$ at $M$ and $N$ meet at $P$. Suppose that $A P$ is parallel to $B C$, $A P=9$ and $P N=15$. Find $A C$.
|
20 \sqrt{2}
|
Answer: $20 \sqrt{2}$
Solution: Extend rays $P M$ and $C B$ to meet at $Q$. Since $A P \| Q C$ and $M$ is the midpoint of $A B$, triangles $A M P$ and $B M Q$ are congruent. This gives $Q M=M P=P N=15$ and $Q B=A P=9$. Observe that the circumcircle of triangle $B M N$ is tangent to $Q M$, so by power of a point, we compute $Q M^{2}=Q B \cdot Q N$, which yields $Q N=25$. Applying Stewart's theorem on triangle $Q N P$, we have
$$
15 \cdot 15^{2}+15 \cdot 25^{2}=30 \cdot 15 \cdot 15+30 M N^{2} \text {, }
$$
which implies that $M N^{2}=\frac{1}{2}\left(25^{2}-15^{2}\right)=200$. Hence, as $M N$ is the midline of triangle $A B C$, we obtain $A C^{2}=4 M N^{2}=800$ and $A C=20 \sqrt{2}$.
| 6
|
6. In trapezoid $\mathrm{PQRS}$, it is known that $\angle \mathrm{PQR}=90^{\circ}, \angle Q R S>90^{\circ}$, diagonal $S Q$ is 24 and is the bisector of angle $S$, and the distance from vertex $R$ to line $Q S$ is 5. Find the area of trapezoid PQRS.
|
\frac{27420}{169}
|
Answer: $\frac{27420}{169}$.
Solution $\angle \mathrm{RQS}=\angle \mathrm{PSQ}$ as alternate interior angles, so triangle $\mathrm{RQS}$ is isosceles. Its height $\mathrm{RH}$ is also the median and equals 5. Then $S R=\sqrt{R H^{2}+S H^{2}}=13$. Triangles SRH and SQP are similar by two angles, the similarity coefficient is $\frac{S R}{S Q}=\frac{13}{24}$. Therefore, $P Q=\frac{24}{13} R H=\frac{120}{13}$, $P S=\frac{24}{13} S H=\frac{288}{13} \cdot$ The area of the trapezoid is $P Q \cdot \frac{Q R+P S}{2}=\frac{27420}{169}$.
| 6
|
97. There are 5 parts that are indistinguishable in appearance, 4 of which are standard and of the same mass, and one is defective, differing in mass from the others. What is the minimum number of weighings on a balance scale without weights that are needed to find the defective part?
|
3
|
$\triangle$ Let's number the parts. Now try to figure out the weighing scheme presented below (Fig. 32).
As can be seen from this, it took three weighings to find the defective part.
Answer: in three.
| 3
|
12. (6 points) There are 1997 odd numbers, the sum of which equals their product. Among them, three numbers are not 1, but three different prime numbers. Then, these three prime numbers are $\qquad$、$\qquad$、$\qquad$.
|
5, 7, 59
|
【Solution】Solution: According to the problem, we have: $1994+a+b+c=a b c$; when $a=3, b=5$, $15 c=c+2002, c=143$, which is not a prime number; when $a=3, b=7$, $21 c=c+2004, c=50 \frac{1}{5}$, which is not an integer; when $a=5, b=7$, $35 c=c+2006, c=59$, which satisfies the condition; therefore, the answer is: $5, 7, 59$.
| 5.5
|
10. Color the 6 regions $A, B, C, D, E, F$ in Figure 1, with each region being colored with 1 color, and no two adjacent regions having the same color. If there are 4 colors available, then there are $\qquad$ different coloring schemes.
|
96
|
10. 96
$A, B, C$ have different colors from each other. They have $4 \times$ $3 \times 2=24$ ways of coloring.
For any one of these (let's assume $A-a \quad B-b \quad C-c$. The other color is $d$), then $D$ can be colored with $b, d$, $E$ can be colored with $c, d$, and $F$ can be colored with $a, d$.
Since $D, E, F$ are adjacent to each other, at most 1 can be colored with $d$, so there are $1+3=4$ ways of coloring, thus the total number of different coloring methods is $4 \times 24=96$.
| 2.67
|
Given positive integers $a$, $b$, and $c$ satisfy $a^{2}+b^{2}-c^{2}=2018$.
Find the minimum values of $a+b-c$ and $a+b+c$.
|
2 \text{ and } 52
|
From the problem, we know
$$
a^{2}+b^{2}=c^{2}+2018 \equiv 2 \text { or } 3(\bmod 4)
$$
$\Rightarrow a, b$ are odd, $c$ is even
$$
\begin{array}{l}
\Rightarrow c^{2}+2018=a^{2}+b^{2} \equiv 2(\bmod 8) \\
\Rightarrow c^{2} \equiv 0(\bmod 8) \Rightarrow 4 \mid c .
\end{array}
$$
Notice,
$$
(a+b)^{2}-c^{2}>a^{2}+b^{2}-c^{2}=2018>0 \text {. }
$$
Therefore, $a+b-c>0$.
Since $a+b-c$ is even, thus, $a+b-c \geqslant 2$.
And $1+1009^{2}-1008^{2}=2018$, at this time,
$$
a+b-c=1+1009-1008=2 \text {. }
$$
Thus, the minimum value of $a+b-c$ is 2.
(1) If $c=4$, then
$$
\begin{array}{l}
(a+b)^{2}>a^{2}+b^{2}=c^{2}+2018>45^{2} \\
\Rightarrow a+b \geqslant 46 ;
\end{array}
$$
If $a+b=46$, then
$$
a^{2}+b^{2}=a^{2}+(46-a)^{2}=2034
$$
$\Rightarrow a^{2}-46 a+41=0$, this equation has no integer solutions;
If $a+b=48$, then
$$
\begin{array}{l}
a^{2}+b^{2}=a^{2}+(48-a)^{2}=2034 \\
\Rightarrow a^{2}-48 a+135=0 \Rightarrow a=3 \text { or } 45 \\
\Rightarrow a+b+c=52 ;
\end{array}
$$
If $a+b \geqslant 50$, then $a+b+c \geqslant 54$.
(2) If $c \geqslant 8$, similarly, $a+b \geqslant 46$, hence
$$
a+b+c \geqslant 46+8=54 \text {. }
$$
In summary, the minimum value of $a+b-c$ is $2$, and the minimum value of $a+b+c$ is 52.
| 3.25
|
The Dingoberry Farm is a 10 mile by 10 mile square, broken up into 1 mile by 1 mile patches. Each patch is farmed either by Farmer Keith or by Farmer Ann. Whenever Ann farms a patch, she also farms all the patches due west of it and all the patches due south of it. Ann puts up a scarecrow on each of her patches that is adjacent to exactly two of Keith's patches (and nowhere else). If Ann farms a total of 30 patches, what is the largest number of scarecrows she could put up?
|
7
|
Whenever Ann farms a patch $P$, she also farms all the patches due west of $P$ and due south of $P$. So, the only way she can put a scarecrow on $P$ is if Keith farms the patch immediately north of $P$ and the patch immediately east of $P$, in which case Ann cannot farm any of the patches due north of $P$ or due east of $P$. That is, Ann can only put a scarecrow on $P$ if it is the easternmost patch she farms in its east-west row, and the northernmost in its north-south column. In particular, all of her scarecrow patches are in different rows and columns. Suppose that she puts up $n$ scarecrows. The farthest south of these must be in the 10th row or above, so she farms at least 1 patch in that column; the second-farthest south must be in the 9th row above, so she farms at least 2 patches in that column; the third-farthest south must be in the 8th row or above, so she farms at least 3 patches in that column, and so forth, for a total of at least $$1+2+\cdots+n=n(n+1) / 2$$ patches. If Ann farms a total of $30<8 \cdot 9 / 2$ patches, then we have $n<8$. On the other hand, $n=7$ scarecrows are possible, as shown.
| 7
|
Let $x_{1}=y_{1}=x_{2}=y_{2}=1$, then for $n \geq 3$ let $x_{n}=x_{n-1} y_{n-2}+x_{n-2} y_{n-1}$ and $y_{n}=y_{n-1} y_{n-2}- x_{n-1} x_{n-2}$. What are the last two digits of $\left|x_{2012}\right|$ ?
|
84
|
Let $z_{n}=y_{n}+x_{n} i$. Then the recursion implies that: $$\begin{aligned} & z_{1}=z_{2}=1+i \\ & z_{n}=z_{n-1} z_{n-2} \end{aligned}$$ This implies that $$z_{n}=\left(z_{1}\right)^{F_{n}}$$ where $F_{n}$ is the $n^{\text {th }}$ Fibonacci number $\left(F_{1}=F_{2}=1\right)$. So, $z_{2012}=(1+i)^{F_{2012}}$. Notice that $$(1+i)^{2}=2 i$$ Also notice that every third Fibonnaci number is even, and the rest are odd. So: $$z_{2012}=(2 i)^{\frac{F_{2012}-1}{2}}(1+i)$$ Let $m=\frac{F_{2012}-1}{2}$. Since both real and imaginary parts of $1+i$ are 1 , it follows that the last two digits of $\left|x_{2012}\right|$ are simply the last two digits of $2^{m}=2^{\frac{F_{2012}-1}{2}}$. By the Chinese Remainder Theorem, it suffices to evaluate $2^{m}$ modulo 4 and 25 . Clearly, $2^{m}$ is divisible by 4 . To evaluate it modulo 25, it suffices by Euler's Totient theorem to evaluate $m$ modulo 20. To determine $\left(F_{2012}-1\right) / 2$ modulo 4 it suffices to determine $F_{2012}$ modulo 8. The Fibonacci sequence has period 12 modulo 8 , and we find $$\begin{aligned} F_{2012} & \equiv 5 \quad(\bmod 8) \\ m & \equiv 2 \quad(\bmod 4) \end{aligned}$$ $2 * 3 \equiv 1(\bmod 5)$, so $$m \equiv 3 F_{2012}-3 \quad(\bmod 5)$$ The Fibonacci sequence has period 20 modulo 5 , and we find $$m \equiv 4 \quad(\bmod 5)$$ Combining, $$\begin{aligned} m & \equiv 14 \quad(\bmod 20) \\ 2^{m} & \equiv 2^{14}=4096 \equiv 21 \quad(\bmod 25) \\ \left|x_{2012}\right| & \equiv 4 \cdot 21=84 \quad(\bmod 100) \end{aligned}$$
| 7.4
|
In a round-robin tournament, 23 teams participated. Each team played exactly once against all the others. We say that 3 teams have cycled victories if, considering only their games against each other, each of them won exactly once. What is the maximum number of cycled victories that could have occurred during the tournament?
|
506
|
Let's solve the problem more generally for $n$ teams, where $n$ is an odd number. We will represent each team with a point. After a match between two teams, an arrow should point from the losing team to the winning team. (In this context, we can assume that there has never been a tie.)
If the teams $A$, $B$, and $C$ have beaten each other in a cycle, which can happen in two ways, then the triangle $ABC$ is called directed. Otherwise, the triangle is not directed.
Provide an estimate for the number of non-directed triangles.
In every non-directed triangle, there is exactly one vertex such that the team represented by this vertex has beaten the other two. We will count the non-directed triangles according to the "winning" vertex.
Let the teams be represented by the points $A_{1}, A_{2}, \ldots, A_{n}$, and let $d_{i}$ denote the number of wins for $A_{i}$. Since there were a total of $\binom{n}{2}$ matches, $\sum_{i=1}^{n} d_{i}=\frac{n(n-1)}{2}$. Then, $\binom{d_{i}}{2}$ non-directed triangles are associated with the vertex $A_{i}$, since we need to choose two from the teams it has beaten.
Thus, the total number of non-directed triangles is: $\sum_{i=1}^{n}\binom{d_{i}}{2}$.
By the inequality between the arithmetic mean and the quadratic mean:
$$
\begin{gathered}
\sum_{i=1}^{n}\binom{d_{i}}{2}=\frac{1}{2} \sum_{i=1}^{n} d_{i}^{2}-\frac{1}{2} \sum_{i=1}^{n} d_{i}=\frac{1}{2} n \frac{\sum_{i=1}^{n} d_{i}^{2}}{n}-\frac{1}{2} \sum_{i=1}^{n} d_{i} \geq \frac{1}{2} n\left(\frac{\sum_{i=1}^{n} d_{i}}{n}\right)^{2}-\frac{1}{2} \sum_{i=1}^{n} d_{i}= \\
=\frac{1}{2} n\left(\frac{n-1}{2}\right)^{2}-\frac{1}{2} \frac{n(n-1)}{2}=\frac{n^{3}-4 n^{2}+3 n}{8}
\end{gathered}
$$
Can equality hold here? Yes, if we can provide a directed complete graph for which
$$
d_{1}=d_{2}=\cdots=d_{n}=\frac{n-1}{2}
$$
Let $n=2 k+1$. Then one possible construction is as follows:
If $1 \leq i<j \leq 2 k+1$ and $j-i$ is greater than $k$, then $A_{j}$ beat $A_{i}$, otherwise $A_{i}$ beat $A_{j}$. It is easy to verify that in this case,
$$
d_{1}=d_{2}=\cdots=d_{n}=\frac{n-1}{2}
$$
Since there are $\binom{n}{3}$ triangles in total, the number of directed triangles in our case is
$$
\binom{n}{3}-\frac{n^{3}-4 n^{2}+3 n}{8}=\frac{n(n-1)(n-2)}{6}-\frac{n^{3}-4 n^{2}+3 n}{8}=\frac{n^{3}-n}{24}
$$
For the case $n=23$, this is 506, so at most 506 cycles of wins could have occurred during the tournament.
Based on the work of András Juhász (Fazekas M. Főv. Gyak. Gimn., 10th grade)
| 5
|
15. (3 points) There are three different sizes of cubic wooden blocks, A, B, and C, where the edge length of A is $\frac{1}{2}$ of the edge length of B, and the edge length of B is $\frac{2}{3}$ of the edge length of C. If A, B, and C blocks are used to form a large cube with the smallest possible volume (using at least one of each type). Then the minimum number of these three types of blocks needed is $\qquad$ blocks.
|
50
|
15. (3 points) There are three different sizes of cubic wooden blocks, A, B, and C, where the edge length of A is $\frac{1}{2}$ of the edge length of B, and the edge length of B is $\frac{2}{3}$ of the edge length of C. If A, B, and C blocks are used to form a large cube with the smallest possible volume (using at least one of each type). Then the minimum number of these three types of blocks needed is 50 _blocks.
【Solution】Let the edge length of A be 1, then the edge length of B is 2, and the edge length of C is 3,
So the volume of A $=1 \times 1 \times 1=1$;
The volume of B $=2 \times 2 \times 2=8$;
The volume of C $=3 \times 3 \times 3=27$;
According to the problem, the smallest edge length of the large cube formed is: $3+2=5$,
Then the smallest volume of the large cube is: $5 \times 5 \times 5=125$,
Based on the analysis and practical operation, when one C block is used, the maximum number of B blocks used is 7,
$$
\begin{array}{l}
125-3 \times 3 \times 3-2 \times 2 \times 2 \times 7, \\
=125-27-56, \\
=42,
\end{array}
$$
So 42 A blocks are needed,
$$
42+1+7=50 \text { (blocks), }
$$
Answer: The minimum number of these three types of blocks needed is 50 blocks.
Therefore, the answer is: 50.
| 3
|
6. Given a string of 2021 letters A and B. Consider the longest palindromic substring. What is its minimum possible length? A palindrome is a string that reads the same from right to left and from left to right.
|
4
|
Solution. The minimum possible length of the maximum palindrome is 4.
We will prove that it cannot be less than 4. Consider the 5 letters in the center of the string. If these are alternating letters, then it is a palindrome of length 5. Suppose among these five letters there are two identical letters standing next to each other. Take the maximal contiguous block of identical letters. It is at least 2 in length, and adding one opposite letter on each side, we get 4 (if there are no other letters on the sides, then we have reached the end of the string and there are many identical letters in a row, since we started from the center of the string).
Let's provide an example of a string where the maximum palindrome has a length of 4. This is a string where the sequence ABABAB repeats periodically: ABABABABABABABABABAB.... By checking all possible positions of the centers of palindromes, one can verify that there are no palindromes longer than 4 in this string. Due to the periodicity of the string, only a small number of cases need to be checked.
Comments. The specified example is unique up to shift and reflection.
| 4
|
10. (5 points) According to the pattern shown in the figure, deduce that $M=$
Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly.
|
1692
|
【Solution】Solution: According to the problem, we have:
First, observe the pattern: $12+3=15$;
$15+5=20 ; \cdots$ Each square plus the circle equals the next number.
At the same time, we notice $20=12+3+5$
$$
27=12+3+5+7
$$
Summarizing the pattern, the numbers in the circles form an arithmetic sequence with the first term 3 and a common difference of 2. Each subsequent square is the sum of all previous numbers.
$$
M=12+3+5+7+9+11+\cdots+81 .
$$
The number of terms is $\frac{81-3}{2}+1=40$.
$$
\begin{array}{l}
M=12+\frac{3+81}{2} \times 40 \\
=12+84 \times 20 \\
=1692
\end{array}
$$
Therefore, the answer is: 1692
| 6.25
|
Example 78. A triangular pyramid is cut by a plane into two polyhedra. We will find the ratio of the volumes of these polyhedra, given that the cutting plane divides the edges converging at one vertex of the pyramid in the ratio $1: 2, 1: 2, 2: 1$, counting from this vertex.
Construction of the image. Let the quadrilateral $S A B C$ with its diagonals be the image of the given pyramid (Fig. 87), $\triangle P Q R$ - the image of the given section. This image is complete, and what is quite curious, no parameter has been spent on it.
Given: $\quad S A B C$ - pyramid, $\quad S$ - vertex, $\quad P \in[S A]$, $Q \in[A B]$, $\quad R \in[A C]$, $\quad|A Q|:|Q B|=1: 2,|A R|:|R C|=1: 2$, $|A P|:|P S|=2: 1,(P Q R)$ - cutting plane.
To find: $V_{1}: V_{2}$ - the ratio of the volumes of the resulting polyhedra.
|
25:2
|
Solution. Let $V$ be the volume of the pyramid $SABC$, and $V_{1}$ the volume of the pyramid $PAQR$. Then $V_{1}=V-V_{2}$.
Construct $[SO]$ and assume that $[SO]$ is the image of the height of the pyramid $SABC$ (thus, two parameters are used). Construct $(AO)$ and $[PM] \|[SO]$. Then $M \in (AO)$. To simplify the calculations, let $|AB|=a, |AC|=b$, $|AS|=c, |SO|=H$.
Then $|AQ|=\frac{1}{3} a, |AR|=\frac{1}{3} b, |AP|=\frac{2}{3} c$, and from the similarity of triangles $APM$ and $ASO$ we have: $|PM|=\frac{2}{3} H$. Now let's calculate $V$ and $V_{2}$.
We have:
$$
\begin{aligned}
V & =\frac{1}{3} S_{\triangle ABC} \cdot H=\frac{1}{6} ab \sin \widehat{BAC} \cdot H \\
V_{2} & =\frac{1}{3} S_{\triangle AQR} \cdot \frac{2}{3} H=\frac{1}{81} ab \sin \widehat{BAC} \cdot H
\end{aligned}
$$
Then
$$
V_{1}=V-V_{2}=\frac{25}{162} abH \sin \widehat{BAC}
$$
Thus,
$$
\frac{V_{1}}{V_{2}}=\frac{\frac{25}{162} abH \sin \widehat{BAC}}{\frac{1}{81} abH \sin \widehat{BAC}}=\frac{25}{2}
$$
Investigation. By the problem's meaning, $V > V_{2}$. Therefore, $V_{1}=V-V_{2}>0$ and, consequently, $\frac{V_{1}}{V_{2}}>1$. The found value of $\frac{V_{1}}{V_{2}}$ satisfies this inequality.
Thus, $V_{1}: V_{2}=25: 2$.
## Problems for Independent Solving
244. The base of a parallelepiped is a rhombus $ABCD$, with side length $a$ and an acute angle of $60^{\circ}$. Find the volume of the parallelepiped if the lateral edge is equal to $a$, and $\widehat{A_{1}AB}=\widehat{A_{1}AD}=45^{\circ}$.
245. Each edge of the parallelepiped is equal to $a$. Each of the three planar angles at one of the vertices of the parallelepiped is equal to $2\alpha$. Find the volume of the parallelepiped.
246.
| 2.67
|
A3. A square with a side length of 2 is divided into 4 triangles (see the figure). All 3 shaded triangles have the same area. What is the area of the white triangle?
(A) $\frac{1+\sqrt{5}}{2}$
(B) $\frac{8}{5}$
(C) 2
(D) $3 \sqrt{5}-5$
(E) $6-2 \sqrt{5}$
|
3 \sqrt{5} - 5
|
A3. Let $A, B, C$ and $D$ be the vertices of the square, and let $E$ and $F$ be the vertices of the white triangle (see the figure).
Let $x = |A E|$. Since the right triangles $A E D$ and $F C D$ have one side equal to the side of the square and have the same area, $|C F| = |A E| = x$. If we consider that the triangles $A E D$ and $E B F$ also have the same area, we get $\frac{2 \cdot x}{2} = \frac{(2 - x) \cdot (2 - x)}{2}$. We rearrange the equation to $x^{2} - 6x + 4 = 0$ and solve it as a quadratic equation to get $x = 3 \pm \sqrt{5}$. Since $x < 2$, the correct solution is $x = 3 - \sqrt{5}$. The area of the white triangle is therefore
$$
p = 2^{2} - 3 \cdot \frac{2 \cdot (3 - \sqrt{5})}{2} = 3 \sqrt{5} - 5
$$
| 4
|
Regular octagon $A_1A_2A_3A_4A_5A_6A_7A_8$ is inscribed in a circle of area $1.$ Point $P$ lies inside the circle so that the region bounded by $\overline{PA_1},\overline{PA_2},$ and the minor arc $\widehat{A_1A_2}$ of the circle has area $\tfrac{1}{7},$ while the region bounded by $\overline{PA_3},\overline{PA_4},$ and the minor arc $\widehat{A_3A_4}$ of the circle has area $\tfrac{1}{9}.$ There is a positive integer $n$ such that the area of the region bounded by $\overline{PA_6},\overline{PA_7},$ and the minor arc $\widehat{A_6A_7}$ of the circle is equal to $\tfrac{1}{8}-\tfrac{\sqrt2}{n}.$ Find $n.$
|
504
|
The actual size of the diagram doesn't matter. To make calculation easier, we discard the original area of the circle, \(1\), and assume the side length of the octagon is \(2\).
Let \(r\) denote the radius of the circle, \(O\) be the center of the circle. Then:
\[r^2= 1^2 + \left(\sqrt{2}+1\right)^2= 4+2\sqrt{2}.\]
Now, we need to find the "D" shape, the small area enclosed by one side of the octagon and \(\frac{1}{8}\) of the circumference of the circle:
\[D= \frac{1}{8} \pi r^2 - [A_1 A_2 O]=\frac{1}{8} \pi \left(4+2\sqrt{2}\right)- \left(\sqrt{2}+1\right)\]
Let \(PU\) be the height of \(\triangle A_1 A_2 P\), \(PV\) be the height of \(\triangle A_3 A_4 P\), \(PW\) be the height of \(\triangle A_6 A_7 P\). From the \(\frac{1}{7}\) and \(\frac{1}{9}\) condition we have
\[\triangle P A_1 A_2= \frac{\pi r^2}{7} - D= \frac{1}{7} \pi \left(4+2\sqrt{2}\right)-\left(\frac{1}{8} \pi \left(4+2\sqrt{2}\right)- \left(\sqrt{2}+1\right)\right)\]
\[\triangle P A_3 A_4= \frac{\pi r^2}{9} - D= \frac{1}{9} \pi \left(4+2\sqrt{2}\right)-\left(\frac{1}{8} \pi \left(4+2\sqrt{2}\right)- \left(\sqrt{2}+1\right)\right)\]
which gives \(PU= \left(\frac{1}{7}-\frac{1}{8}\right) \pi \left(4+ 2\sqrt{2}\right) + \sqrt{2}+1\) and \(PV= \left(\frac{1}{9}-\frac{1}{8}\right) \pi \left(4+ 2\sqrt{2}\right) + \sqrt{2}+1\).
Now, let \(A_1 A_2\) intersects \(A_3 A_4\) at \(X\), \(A_1 A_2\) intersects \(A_6 A_7\) at \(Y\),\(A_6 A_7\) intersects \(A_3 A_4\) at \(Z\).
Clearly, \(\triangle XYZ\) is an isosceles right triangle, with right angle at \(X\) and the height with regard to which shall be \(3+2\sqrt2\). Now \(\frac{PU}{\sqrt{2}} + \frac{PV}{\sqrt{2}} + PW = 3+2\sqrt2\) which gives:
\begin{align*}
PW&= 3+2\sqrt2-\frac{PU}{\sqrt{2}} - \frac{PV}{\sqrt{2}} \\
&=3+2\sqrt{2}-\frac{1}{\sqrt{2}}\left(\left(\frac{1}{7}-\frac{1}{8}\right) \pi \left(4+ 2\sqrt{2}\right) + \sqrt{2}+1+\left(\frac{1}{9}-\frac{1}{8}\right) \pi \left(4+ 2\sqrt{2}\right) + \sqrt{2}+1\right)\\
&=1+\sqrt{2}- \frac{1}{\sqrt{2}}\left(\frac{1}{7}+\frac{1}{9}-\frac{1}{4}\right)\pi\left(4+2\sqrt{2}\right)
\end{align*}
Now, we have the area for \(D\) and the area for \(\triangle P A_6 A_7\), so we add them together:
\begin{align*}
\text{Target Area} &= \frac{1}{8} \pi \left(4+2\sqrt{2}\right)- \left(\sqrt{2}+1\right) + \left(1+\sqrt{2}\right)- \frac{1}{\sqrt{2}}\left(\frac{1}{7}+\frac{1}{9}-\frac{1}{4}\right)\pi\left(4+2\sqrt{2}\right)\\
&=\left(\frac{1}{8} - \frac{1}{\sqrt{2}}\left(\frac{1}{7}+\frac{1}{9}-\frac{1}{4}\right)\right)\text{Total Area}
\end{align*}
The answer should therefore be \(\frac{1}{8}- \frac{\sqrt{2}}{2}\left(\frac{16}{63}-\frac{16}{64}\right)=\frac{1}{8}- \frac{\sqrt{2}}{504}\). The answer is \(\boxed{504}\).
SpecialBeing2017
| 6.8
|
A $10\times10\times10$ grid of points consists of all points in space of the form $(i,j,k)$, where $i$, $j$, and $k$ are integers between $1$ and $10$, inclusive. Find the number of different lines that contain exactly $8$ of these points.
|
168
|
$Case \textrm{ } 1:$ The lines are not parallel to the faces
A line through the point $(a,b,c)$ must contain $(a \pm 1, b \pm 1, c \pm 1)$ on it as well, as otherwise, the line would not pass through more than 5 points. This corresponds to the 4 diagonals of the cube.
We look at the one from $(1,1,1)$ to $(10,10,10)$. The lower endpoint of the desired lines must contain both a 1 and a 3, so it can be $(1,1,3), (1,2,3), (1,3,3)$. If $\textrm{min} > 0$ then the point $(a-1,b-1,c-1)$ will also be on the line for example, 3 applies to the other end.
Accounting for permutations, there are $12$ ways, so there are $12 \cdot 4 = 48$ different lines for this case.
$Case \textrm{ } 2:$ The lines where the $x$, $y$, or $z$ is the same for all the points on the line.
WLOG, let the $x$ value stay the same throughout. Let the line be parallel to the diagonal from $(1,1,1)$ to $(1,10,10)$. For the line to have 8 points, the $y$ and $z$ must be 1 and 3 in either order, and the $x$ value can be any value from 1 to 10. In addition, this line can be parallel to 6 face diagonals. So we get $2 \cdot 10 \cdot 6 = 120$ possible lines for this case.
The answer is, therefore, $120 + 48 = \boxed{168}$
Solution by stephcurry added to the wiki by Thedoge edited by Rapurt9 and phoenixfire
| 6.6
|
5. (8 points) Fill in the blanks with $1-6$, so that the numbers in each row and each column are not repeated. The two cells occupied by the same symbol in the figure have the same number combination, but the order is uncertain. Therefore, the five-digit number formed by the first five numbers from left to right in the last row is
保留源文本的换行和格式,直接输出翻译结果。
|
46123
|
46123
【Solution】Solution: According to the problem, we know:
First, the number in the second row and second column can only be 5, and the number in the third row and fourth column can only be 6.
Continuing the reasoning, the solution is as shown in the figure:
Therefore, the answer is: 46123.
| 5
|
22. Let $x>1, y>1$ and $z>1$ be positive integers for which the following equation
$$
1!+2!+3!+\ldots+x!=y^{2}
$$
is satisfied. Find the largest possible value of $x+y+z$.
|
8
|
22. Answer. 8
Solution. We first prove that if $x \geq 8$, then $z=2$. To this end, we observe that the left hand side of the equation $1!+2!+3!+\ldots+x!$ is divisible by 3 , and hence $3 \mid y^{2}$. Since 3 is a prime, $3 \mid y$. So, $3^{z} \mid y^{z}$ by elementary properties of divisibility.
On the other hand, when $x=8$,
$$
1!+2!+\ldots+8!=46233
$$
is divisible by $3^{2}$ but not by $3^{3}$. Now, note that if $n \geq 9$, then we have $3^{3} \mid n!$. So, when $x \geq 8$, the left hand side is divisible by $3^{2}$ but not by $3^{3}$. This means that $z=2$.
We now prove further that when $x \geq 8$, then the given equation has no solutions. To prove this, we observe that $x \geq 8$ implies that
$$
1!+2!+3!+4!+\underbrace{5!+\ldots x!}_{\text {divisisble by } 5} \equiv 3(\bmod 5) .
$$
Since we have deduced that $z=2$, we only have $y^{2} \equiv 0,1,-1 \quad(\bmod 5)$. This mismatch now completes the argument that there are no solutions to the equation when $x \geq 8$.
So the search narrows down to $x<8$. By exhaustion, it is easy to find that there is only one solution:
$$
x=y=3, z=2 .
$$
Thus, the sum of this only combination must be the largest and is equal to $3+3+2=8$.
| 8
|
7.3 Given that a closed broken line is drawn along the grid lines of a square grid paper, consisting of 14 segments and with at most one edge of the broken line on each grid line, how many self-intersection points can this broken line have at most?
untranslated text remains unchanged:
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
|
17
|
[Solution] Since the polyline is drawn along the grid lines, its horizontal and vertical edges are alternately arranged, so among the 14 edges, there must be 7 horizontal edges and 7 vertical edges. Number the horizontal edges from top to bottom as 1 to 7. It is easy to see that there are no self-intersection points on the 1st horizontal edge, at most 2 self-intersection points on the 2nd horizontal edge, and at most 4 self-intersection points on the 3rd horizontal edge. Similarly, there are at most 0, 2, and 4 self-intersection points on the 7th, 6th, and 5th horizontal edges, respectively. For the 4th horizontal edge, there is one vertical edge connected to each end, so there are at most 5 self-intersection points. Therefore, the entire polyline has at most 17 self-intersection points.
On the other hand, the polyline in the right figure has 14 edges, each on a grid line, and has a total of 17 self-intersection points.
In summary, this polyline has at most 17 self-intersection points.
| 6
|
11. Divide the set $M=$ $\{1,2, \cdots, 12\}$ of the first 12 positive integers into four triplets, such that in each triplet, one number is equal to the sum of the other two. Find the number of different ways to do this.
|
8
|
11. Let the four subsets be $M_{i}=\left(a_{i}, b_{i}, c_{i}\right)$, where $a_{i}=b_{i}+c_{i}, b_{i}>c_{i}, i=1,2,3,4$.
Given $a_{1}=27$.
Thus, $10 \leqslant a_{3} \leqslant 11$.
If $a_{3}=10$, then from
$$
a_{1}+a_{2}=17, a_{2}a_{1}+a_{2}=17,
$$
we get $a_{2}=9, a_{1}=8$
$$
\Rightarrow\left(a_{1}, a_{2}, a_{3}, a_{4}\right)=(8,9,10,12) .
$$
From $8=b_{1}+c_{1}, 9=b_{2}+c_{2}, 10=b_{3}+c_{3}$, $12=b_{4}+c_{4}$, we must have
$$
b_{4}=11, c_{4}=1 .
$$
This results in two cases:
$$
\begin{array}{l}
12=11+1,10=7+3,9=5+4,8=6+2 ; \\
12=11+1,10=6+4,9=7+2,8=5+3 .
\end{array}
$$
Corresponding to two partition methods:
$$
\begin{array}{l}
(12,11,1),(10,7,3),(9,5,4),(8,6,2) \text {; } \\
(12,11,1),(10,6,4),(9,7,2),(8,5,3) .
\end{array}
$$
If $a_{3}=11$, then $a_{1}+a_{2}=16$.
Thus $9 \leqslant a_{2} \leqslant 10$
$$
\Rightarrow\left(a_{1}, a_{2}\right)=(6,10),(7,9) \text {. }
$$
For $\left(a_{1}, a_{2}, a_{3}, a_{4}\right)=(6,10,11,12)$, we get three partition methods:
$$
\begin{array}{l}
(12,8,4),(11,9,2),(10,7,3),(6,5,1) ; \\
(12,9,3),(11,7,4),(10,8,2),(6,5,1) ; \\
(12,7,5),(11,8,3),(10,9,1),(6,4,2) .
\end{array}
$$
For $\left(a_{1}, a_{2}, a_{3}, a_{4}\right)=(7,9,11,12)$, we also get three partition methods:
$$
\begin{array}{l}
(12,8,4),(11,10,1),(9,6,3),(7,5,2) ; \\
(12,10,2),(11,6,5),(9,8,1),(7,4,3) ; \\
(12,10,2),(11,8,3),(9,5,4),(7,6,1) .
\end{array}
$$
Therefore, there are a total of eight partition methods for this problem.
| 3
|
11、Given the ellipse $C: \frac{x^{2}}{3}+y^{2}=1$ with its upper vertex $A$, a line $l$ that does not pass through $A$ intersects the ellipse $C$ at points $P$ and $Q$, and $A P \perp A Q$. Find the maximum value of the area of $\triangle A P Q$.
---
Note: The format and line breaks have been preserved as requested.
|
\frac{9}{4}
|
11. Analysis: When the slope of line $P Q$ does not exist, we know that $\angle P A Q$ is an acute angle, which does not meet the problem's requirements. Therefore, we only need to consider the case where the slope exists.
Let $P\left(x_{1}, y_{1}\right), Q\left(x_{2}, y_{2}\right)$, and the equation of line $P Q$ be $y=k x+b$. By combining the ellipse equation $\frac{x^{2}}{3}+y^{2}=1$, and eliminating $y$, we get $\left(k^{2}+\frac{1}{3}\right) x^{2}+2 k b x+b^{2}-1=0$. Thus, $x_{1}+x_{2}=\frac{-2 k b}{k^{2}+\frac{1}{3}}, x_{1} x_{2}=\frac{b^{2}-1}{k^{2}+\frac{1}{3}}$. According to the problem, $A P \perp A Q$, so $A P \cdot A Q=\stackrel{1}{0}$, which means $x_{1} x_{2}+\left(y_{1}-1\right)\left(y_{2}-1\right)=0$. Therefore,
$$
\begin{array}{l}
0=x_{1} x_{2}+\left(y_{1}-1\right)\left(y_{2}-1\right)=x_{1} x_{2}+\left(k x_{1}+b-1\right)\left(k x_{2}+b-1\right)=\left(k^{2}+1\right) x_{1} x_{2}+k(b-1)\left(x_{1}+x_{2}\right)+(b-1)^{2} \\
=\frac{\left(k^{2}+1\right)\left(b^{2}-1\right)}{k^{2}+\frac{1}{3}}-\frac{2 k b(b-1)}{k^{2}+\frac{1}{3}}+(b-1)^{2}=\frac{\left(k^{2}+1\right)\left(b^{2}-1\right)-2 k b(b-1)+(b-1)^{2}\left(k^{2}+\frac{1}{3}\right)}{\left(k^{2}+\frac{1}{3}\right)},
\end{array}
$$
Thus, $\left(k^{2}+1\right)\left(b^{2}-1\right)-2 k b(b-1)+(b-1)^{2}\left(k^{2}+\frac{1}{3}\right)=0$, simplifying to $b=-\frac{1}{2}$. Therefore, the equation of line $P Q$ is $y=k x-\frac{1}{2}$, which always passes through the fixed point $C\left(0,-\frac{1}{2}\right)$. We have $x_{1}+x_{2}=\frac{3 k}{3 k^{2}+1}, x_{1} x_{2}=\frac{-9}{4\left(3 k^{2}+1\right)}$, thus
$$
\left|x_{1}-x_{2}\right|=\sqrt{\left(x_{1}+x_{2}\right)^{2}-4 x_{1} x_{2}}=\sqrt{\left(\frac{3 k}{3 k^{2}+1}\right)^{2}+\frac{9}{\left(3 k^{2}+1\right)}}=\frac{6 \sqrt{k^{2}+\frac{1}{4}}}{3 k^{2}+1} \text {. }
$$
Let $t=\sqrt{k^{2}+\frac{1}{4}}$, then $t \geq \frac{1}{2} \cdot S_{\triangle A P Q}=\frac{1}{2}|A C| \cdot\left|x_{1}-x_{2}\right|=\frac{9 t}{3 t^{2}+\frac{1}{4}}=\frac{9}{3 t+\frac{1}{4 t}}\left(t \geq \frac{1}{2}\right)$, we know that $t=\frac{1}{2}$, i.e., $k=0$, when $S_{\triangle A P Q}$ reaches its maximum value $\frac{9}{4}$. Therefore, the maximum area of $\triangle A P Q$ is $\frac{9}{4}$.
| 5
|
G1.1 In the given diagram, $\angle A+\angle B+\angle C+\angle D+\angle E=a^{\circ}$, find $a$.
|
180
|
$\begin{array}{l}\text { In } \triangle A P Q, \angle B+\angle D=\angle A Q P \ldots \ldots \text { (1) (ext. } \angle \text { of } \triangle) \\ \angle C+\angle E=\angle A P Q \ldots \ldots \text { (2) (ext. } \angle \text { of } \triangle) \\ \begin{array}{l} \angle A+\angle B+\angle C+\angle D+\angle E=\angle A+\angle A Q P+\angle A P Q \text { (by (1) and (2)) } \\ \quad=180^{\circ}(\angle \mathrm{s} \text { sum of } \triangle)\end{array} \\ \begin{aligned} \therefore a=180\end{aligned}\end{array}$
| 1
|
6. To reduce heating costs in a residential building, the tenants decided to change the facade, and they were granted non-repayable funds from the Environmental Protection and Energy Efficiency Fund, which cover 60% of all total costs. The total cost for the new facade is 1,200,000 kn. The new facade guarantees that the average annual heating costs will be reduced by 35%. If the average annual heating cost for the building was 168,000 kn, how many years will it take for this investment to pay off?
|
9
|
6. The cost for the facade is 1200000 kn. The non-refundable portion of funds is $60\%$, which means that the residents have to cover $40\%$ of the costs, amounting to $480000 \mathrm{kn}$.
1 POINT
The average annual heating cost was 168000 kn, and with a savings of 35%, it will amount to 109200 kn.
1 POINT
Let $n$ be the number of years needed for the investment to pay off. Then the total cost for $n$ years of heating before the new facade is $168000 n$,
and the total cost for $n$ years of heating after the new facade is $109200 n$.
1 POINT
We need to determine the smallest number of years for which the heating cost before the new facade will be greater than the sum of the total heating costs after the new facade and the costs for the facade paid by the residents.
Determine the smallest natural number $n$ for which the following holds:
$168000 n > 109200 n + 480000$.
1 POINT
$168000 n - 109200 n > 480000$
$58800 n > 480000$
1 POINT
$n > \frac{480000}{58800}$
1 POINT
Since $\frac{480000}{58800} \approx 8.2$,
1 POINT
the smallest natural number that satisfies this condition is 9, meaning the investment will pay off in 9 years.
| 1
|
Three squares are attached to each other by their vertices and to two vertical rods, as shown in the figure. Determine the measure of angle $x$.
#
|
39^{\circ}
|
Solution
In the drawing below, where $AB$ is parallel to $CD$, we will show that the sum of the white angles is equal to the sum of the measures of the gray angles. This result holds for any number of "peaks" in the drawing and is popularly known as the "Theorem of Peaks".
At each vertex of the "peaks," draw a line parallel to the segment $AB$. Notice that several pairs of alternate interior angles, which are congruent, will be formed as indicated in the figure below.
Each of the marked angles has exactly one representative among the white and gray angles. Thus, each of these sums of angle measures is $x_{1}+x_{2}+\ldots+x_{6}$.
Since the two vertical bars are parallel, we can apply the Theorem of Peaks to the polygonal path formed by the sides of the squares containing the marked angles, obtaining:
$$
30^{\circ}+126^{\circ}+75^{\circ}+x=90^{\circ}+90^{\circ}+90^{\circ}
$$
Thus, $x=39^{\circ}$.
| 3
|
4. Let $A$ and $B$ be the vertices of the major axis of the ellipse $\Gamma$, $E$ and $F$ be the two foci of $\Gamma$, $|A B|=4,|A F|=2+\sqrt{3}$, and $P$ be a point on $\Gamma$ such that $|P E||P F|=2$. Then the area of $\triangle P E F$ is $\qquad$
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
1
|
4.1.
Let's assume the standard equation of the parabola $\Gamma$ in the Cartesian coordinate system is $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$.
According to the conditions, we have $2 a=|A B|=4$,
$a \pm \sqrt{a^{2}-b^{2}}=|A F|=2+\sqrt{3}$.
Thus, $a=2, b=1$, and $|E F|=2 \sqrt{a^{2}-b^{2}}=2 \sqrt{3}$.
By the definition of an ellipse, we know $|P E|+|P F|=2 a=4$.
Also, $|P E||P F|=2$, so we get
$|P E|^{2}+|P F|^{2}$
$=(|P E|+|P F|)^{2}-2|P E||P F|$
$=12=|E F|^{2}$.
Therefore, $\angle E P F=90^{\circ}$.
Thus, $S_{\triangle P E F}=\frac{1}{2}|P E||P F|=1$.
| 4
|
8. There are two teams competing, and the probability of each team winning a match is $\frac{1}{2}$. It is stipulated that a team must win four consecutive matches to end the series. The number of matches played is a random variable $\xi$, then the expected value E $\xi=$ $\qquad$ .
|
\frac{27}{2}
|
8. $\frac{27}{2}$.
Let the probability that the match ends exactly after the $k(k \geqslant 1)$-th game be $p_{k}$. Then
$$
p_{1}=0, p_{2}=0, p_{3}=0, p_{4}=\frac{1}{2^{3}} \text {. }
$$
When $n \geqslant 6$,
$$
\begin{array}{l}
p_{n-1}=\frac{1}{2} p_{n-2}+\frac{1}{2^{2}} p_{n-3}+\frac{1}{2^{3}} p_{n-4} \\
p_{n}=\frac{1}{2} p_{n-1}+\frac{1}{2^{2}} p_{n-2}+\frac{1}{2^{3}} p_{n-3} .
\end{array}
$$
$$
\begin{array}{l}
\text { (2) }-\frac{1}{2} \times(1) \text { gives } \\
p_{n}=p_{n-1}-\frac{1}{2^{4}} p_{n-4}(n \geqslant 6) .
\end{array}
$$
$$
\begin{array}{l}
\text { Then } \mathrm{E} \xi=\sum_{k>4} k p_{k} \\
=4 p_{4}+5 p_{5}+\sum_{k \geqslant 6} k\left(p_{k-1}-\left(\frac{1}{2}\right)^{4} p_{k-4}\right) \\
=4 p_{4}+5 p_{5}+\sum_{k \geqslant 6} k p_{k-1}-\left(\frac{1}{2}\right)^{4} \sum_{k \geqslant 8} k p_{k-4} \\
=4 p_{4}+5 p_{5}+\sum_{k \geqslant 6} k p_{k-1}- \\
\left(\frac{1}{2}\right)^{4} \sum_{k \geq 5}(k+3) p_{k-1} \\
=4 p_{4}+5 p_{5}-8 \times\left(\frac{1}{2}\right)^{4} p_{4}+ \\
\sum_{k \geqslant 6}\left(k-\left(\frac{1}{2}\right)^{4}(k+3)\right) p_{k-1} \\
=4 p_{4}+5 p_{5}-8 \times\left(\frac{1}{2}\right)^{4} p_{4}+ \\
\sum_{k \geqslant 5}\left((k+1)-\left(\frac{1}{2}\right)^{4}(k+4)\right) p_{k} \\
=5 p_{5}-p_{4}+\sum_{k \geqslant 4}\left((k+1)-\left(\frac{1}{2}\right)^{4}(k+4)\right) p_{k} \\
=5 p_{5}-p_{4}+\left(1-\left(\frac{1}{2}\right)^{4}\right) \sum_{k \geqslant 4} k p_{k}+ \\
\left(1-4 \times\left(\frac{1}{2}\right)^{4}\right) \sum_{k \geqslant 4} p_{k} \text {. } \\
\end{array}
$$
Notice that, $p_{4}=\frac{1}{2^{3}}, p_{5}=\frac{1}{2^{4}}$,
$$
\sum_{k \geqslant 5} p_{k}=1-\left(p_{1}+p_{2}+p_{3}+p_{4}\right)=1-\left(\frac{1}{2}\right)^{3} \text {. }
$$
Thus, E $\xi=\left(5 \times \frac{1}{2^{4}}-\left(\frac{1}{2}\right)^{3}+\right.$
$$
\begin{aligned}
& \left.\left(1-4 \times\left(\frac{1}{2}\right)^{4}\right)\left(1-\left(\frac{1}{2}\right)^{3}\right)\right) \times 2^{4} \\
= & \frac{27}{2} .
\end{aligned}
$$
| 5.5
|
9.
\begin{tabular}{ll}
Across & Down \\
1. A square & 1. Twice a fifth power \\
3. A fourth power & 2. A cube
\end{tabular}
When completed correctly, the cross number is filled with four three-digit numbers. What digit is *?
A 0
B 1
C 2
D 4
E 6
|
4
|
Solution
D
When you are faced with a crossnumber, the best strategy is to look for clues where it is easy to find a unique solution.
Among the three-digit integers there are more squares and cubes than fourth and fifth powers. So the best strategy is to begin with 1 Down and 3 Across.
The first few numbers that are twice fifth powers are $2 \times 1^{5}=2 \times 1=2$, $2 \times 2^{5}=2 \times 32=64,2 \times 3^{5}=2 \times 243=486$ and $2 \times 4^{5}=2 \times 1024=2048$.
We can deduce from this that 486 which is the only three-digit number in this list is the answer for 1 Down.
It follows that 3 Across is a three-digit fourth power with 6 as its hundreds digit. We have $3^{4}=81,4^{4}=256,5^{4}=625$ and $6^{4}=1296$.
We deduce that 3 Across is 625 .
We now see that 2 Down is three-digit cube with units digit 5 . Hence 2 Down is is $5^{3}=125$.
Finally, 1 Across is a three-digit square with hundreds digit 4 and units digit 1. Therefore 1 Across is $21^{2}=441$.
We can now deduce that $*$ is 4 .
| 2
|
9. (12 points) Three people, A, B, and C, depart from location $A$ to location $B$. A departs at 8:00, B at 8:20, and C at 8:30. They all travel at the same speed. 10 minutes after C departs, the distance from A to $B$ is exactly half the distance from B to $B$. At this moment, C is 2015 meters away from $B$. Therefore, the distance between $A$ and $B$ is $\qquad$ meters.
|
2418
|
9. (12 points) Three people, A, B, and C, depart from location $A$ to location $B$. A departs at 8:00, B at 8:20, and C at 8:30. They all travel at the same speed. 10 minutes after C departs, the distance from A to $B$ is exactly half the distance from B to $B$. At this time, C is 2015 meters away from $B$, and the distance between $A$ and $B$ is 2418 meters.
【Solution】Solution: According to the problem, we know:
Let the distance B and C travel in 10 minutes be 1 unit;
The distance A and B travel in 20 minutes is 2 units;
The distance from A to $B$ is the same as the distance from A to B, which is also 2 units.
Therefore, the distance from C to $B$ is 5 units, corresponding to 2015 meters, so 1 unit is $2015 \div 5 = 403$ meters.
The distance between B and C is also the distance C travels in 10 minutes, which is 1 unit. Therefore, the total distance is 6 units, which is: $403 \times 6 = 2418$ meters.
Thus, the answer is: 2418.
| 2.67
|
We create a "die" from a spherical object by cutting off six equal spherical caps in such a way that the circles formed where the spherical caps were removed each touch four of their neighbors. What percentage of the total surface area of the die is the combined area of the six circles?
How many percent of the total surface area of the die is the combined area of the six circles?
|
86.08\%
|
Solution. Let the radius of the sphere be denoted by $R$, its center by $O$, and the radius of the circular faces by $r$. Consider one of the circular faces, and let the two opposite points of tangency on this face be $A$ and $B$.

The plane $OAB$, due to the symmetry of the sphere and the cube, cuts a square out of the cube, with the side length of the square being $2r$. The length of the diagonal $AC$ is $AC = 2r\sqrt{2}$, hence $AO = \frac{AC}{2} = r\sqrt{2} = R$. The total area of the six circular faces is:
$$
t = 6r^2\pi = 6\left(\frac{R\sqrt{2}}{2}\right)^2\pi = 3R^2\pi
$$
Now, let's calculate the total surface area $F$ of the cube. The surface area is obtained by subtracting the surface area of the six spherical caps from the surface area of the sphere $F_{\text{g}} = 4R^2\pi$ and adding the area of the six circular faces. The surface area of one spherical cap is $F_1 = 2\pi Rm$, where $R$ is the radius of the sphere and $m$ is the height of the spherical cap: $m = R - r$, where $r = \frac{R\sqrt{2}}{2}$,
$$
\begin{aligned}
& m = \left(R - \frac{R\sqrt{2}}{2}\right) = R\left(1 - \frac{\sqrt{2}}{2}\right), \quad \text{and} \\
& F_1 = 2\pi R^2\left(1 - \frac{\sqrt{2}}{2}\right) = R^2\pi(2 - \sqrt{2})
\end{aligned}
$$
Thus, the surface area of the cube is:
$$
\begin{aligned}
F & = 4R^2\pi - 6R^2\pi(2 - \sqrt{2}) + 3R^2\pi = \\
& = R^2\pi(4 - 12 + 6\sqrt{2} + 3) = R^2\pi(6\sqrt{2} - 5)
\end{aligned}
$$
Finally, let's calculate what percentage of the total surface area of the cube is covered by the six circular faces:
$$
\frac{3R^2\pi}{R^2\pi(6\sqrt{2} - 5)} = \frac{3(6\sqrt{2} + 5)}{47} \approx 86.08\%
$$
| 5
|
Task 2. What is $\frac{31}{71}$ of the number
$$
\frac{1-\frac{1}{3}:\left(2+\frac{1}{6}\right)}{3 \frac{2}{5}+\frac{10-\frac{1}{4}}{3}: \frac{5}{8}} \cdot 8 \frac{3}{5}-\frac{1.5 \cdot \frac{15}{4} \cdot 2.5+\frac{3}{5-\frac{2}{3}}}{1+\frac{1}{7}+\frac{6}{\frac{12}{11} \cdot\left(\frac{8}{3}-\frac{7}{4}\right) \cdot 7}} ?
$$
|
0
|
Solution. Let's first calculate the value of the given expression. We have:
$$
\begin{aligned}
& \frac{1-\frac{1}{3}:\left(2+\frac{1}{6}\right)}{3 \frac{2}{5}+\frac{10-\frac{1}{4}}{3}: \frac{5}{8}} \cdot 8 \frac{3}{5}-\frac{1.5: \frac{15}{4} \cdot 2.5+\frac{3}{5-\frac{2}{3}}}{1+\frac{1}{7}+\frac{6}{\frac{12}{11} \cdot\left(\frac{8}{3}-\frac{7}{4}\right) \cdot 7}}=\frac{1-\frac{1}{3} \cdot \frac{13}{6}}{\frac{17}{5}+\frac{39}{3} \cdot \frac{8}{5}} \cdot \frac{43}{5}-\frac{\frac{3}{2} \cdot \frac{4}{11} \cdot \frac{5}{2}+\frac{3}{\frac{13}{3}}}{\frac{8}{7}+\frac{6}{\frac{12}{11} \cdot \frac{11}{12} \cdot 7}} \\
& =\frac{1-\frac{2}{13}}{\frac{17}{5}+\frac{13}{4} \cdot \frac{8}{5}} \cdot \frac{43}{5}-\frac{1+\frac{9}{13}}{\frac{8}{7}+\frac{6}{7}} \\
& =\frac{\frac{11}{13}}{\frac{17}{5}+\frac{26}{5}} \cdot \frac{43}{5}-\frac{\frac{22}{13}}{\frac{14}{7}} \\
& =\frac{5 \cdot 11}{13 \cdot 43} \cdot \frac{43}{5}-\frac{11}{13}=0
\end{aligned}
$$
Finally, $\frac{31}{71}$ of 0 is 0.
| 2
|
Define a sequence $a_{i, j}$ of integers such that $a_{1, n}=n^{n}$ for $n \geq 1$ and $a_{i, j}=a_{i-1, j}+a_{i-1, j+1}$ for all $i, j \geq 1$. Find the last (decimal) digit of $a_{128,1}$.
|
4
|
By applying the recursion multiple times, we find that $a_{1,1}=1, a_{2, n}=n^{n}+(n+1)^{n+1}$, and $a_{3, n}=n^{n}+2(n+1)^{n+1}+(n+2)^{n+2}$. At this point, we can conjecture and prove by induction that $a_{m, n}=\sum_{k=0}^{m-1}\binom{m-1}{k}(n+k)^{n+k}=\sum_{k \geq 0}\binom{m-1}{k}(n+k)^{n+k}$. (The second expression is convenient for dealing with boundary cases. The induction relies on $\binom{m}{0}=\binom{m-1}{0}$ on the $k=0$ boundary, as well as $\binom{m}{k}=\binom{m-1}{k}+\binom{m-1}{k-1}$ for $k \geq 1$.) We fix $m=128$. Note that $\binom{127}{k} \equiv 1(\bmod 2)$ for all $1 \leq k \leq 127$ and $\binom{127}{k} \equiv 0(\bmod 5)$ for $3 \leq k \leq 124$, by Lucas' theorem on binomial coefficients. Therefore, we find that $a_{128,1}=\sum_{k=0}^{127}\binom{127}{k}(k+1)^{k+1} \equiv \sum_{k=0}^{127}(k+1)^{k+1} \equiv 0 \quad(\bmod 2)$ and $a_{128,1} \equiv \sum_{k \in[0,2] \cup[125,127]}\binom{127}{k}(k+1)^{k+1} \equiv 4 \quad(\bmod 5)$. Therefore, $a_{128,1} \equiv 4(\bmod 10)$.
| 7.25
|
Example 14 Let $X=\left\{A_{1}, A_{2}, \cdots, A_{n}\right\}$ be a family of distinct three-element subsets of $I=\{1,2,3, \cdots, 36\}$, satisfying:
(1) For any $1 \leqslant i<j \leqslant n, A_{i} \cap A_{j} \neq \varnothing$,
(2) $A_{1} \cap A_{2} \cap \cdots \cap A_{n}=\varnothing$.
Find the maximum value of $n$, and how many different families $X$ are there when $n$ reaches its maximum value?
|
(100, 34 C_{36}^{3})
|
Let $X$ satisfy the conditions of the problem, and without loss of generality, let $A_{1}=\{1,2,3\}$. By condition (2), there exists an element of $X$ that does not contain 1, and we can assume $A_{2}=\left\{a_{1}, a_{2}, a_{3}\right\}$, and $1 \notin A_{2}$. Similarly, we can set $A_{3}=\left\{b_{1}, b_{2}, b_{3}\right\}$, and $2 \notin A_{3}$, $A_{4}=\left\{c_{1}, c_{2}, c_{3}\right\}$, and $3 \notin A_{4}$. By condition (1), each element of $X$ must contain at least one of the following 9 pairs as a subset:
$\left\{1, a_{1}\right\},\left\{1, a_{2}\right\},\left\{1, a_{3}\right\},\left\{2, b_{1}\right\},\left\{2, b_{2}\right\},\left\{2, b_{3}\right\},\left\{3, c_{1}\right\},\left\{3, c_{2}\right\},\left\{3, c_{3}\right\}$. Since $|I|=36$, each of these pairs can be a subset of at most $36-2=34$ elements of $X$.
If there do not exist 3 pairs such that each pair is a subset of at least 4 elements of $X$, then at most 2 pairs can be subsets of 34 elements of $X$, and the remaining 7 pairs can be subsets of at most 3 elements of $X$. Therefore,
$n=|X| \leqslant 2 \times 34 + 7 \times 3 = 89$.
Now assume that among these 9 pairs, there are at least 3 pairs such that each pair is a subset of at least 4 elements of $X$. Let these 3 pairs be $p_{1}=\{a, b\}, p_{2}=\{c, d\}, p_{3}=\{e, f\}$.
Since $p_{1}$ is a subset of at least 4 elements of $X$, $\{a, b, x\},\{a, b, y\},\{a, b, z\},\{a, b, w\}$, and any other element $A$ of $X$ must share at least one common element with these 4 elements, which can only be $a$ or $b$ (otherwise, $A$ would contain 4 different elements $x, y, z, w$, which is a contradiction). Similarly, this applies to $p_{2}$ and $p_{3}$.
If $p_{1} \cap p_{2}=\varnothing$, then there must be two elements of $X$ of the form $\{a, b, x\}$ and $\{c, d, y\}$ (where $x \neq c, d, y, y \neq a, b, x$), which contradicts condition (1). Therefore, $p_{1}, p_{2}, p_{3}$ must have non-empty intersections.
We consider two cases:
( I ) $p_{1} \cap p_{2} \cap p_{3} \neq \varnothing$, let $p_{1}=\{x, y\}, p_{2}=\{x, z\}, p_{3}=\{x, w\}$. Here, $x, y, z, w \in I$. Thus, the elements of $X$ that do not contain $x$ can only be $\{y, z, w\}$. Therefore, $\{y, z, w\}$ is an element of $X$ and $X \subseteq Y(x, y, z, w)$, where $Y(x, y, z, w)$ is the set of all 3-element subsets that contain $x$ and at least one of $y, z, w$. Thus, $n=|X| \leqslant |Y(x, y, z, w)| = 1 + C_{3}^{2} + C_{3}^{1} C_{32}^{1} = 100$, with equality holding if and only if $X = Y(x, y, z, w)$. There are $C_{36}^{3} \cdot C_{33}^{1} = C_{36}^{1} \cdot C_{35}^{3} = 33 \cdot C_{36}^{3}$ such $X = Y(x, y, z, w)$.
( II ) $p_{1} \cap p_{2} \cap p_{3} = \varnothing$. Since $p_{1}, p_{2}, p_{3}$ have non-empty intersections, we can set $p_{1}=\{x, y\}, p_{2}=\{y, z\}, p_{3}=\{x, z\}$, where $x, y, z \in I$. Thus, each element of $X$ must contain at least 2 of $x, y, z$, so $X \subseteq Y(x, y, z)$, where $Y(x, y, z)$ is the set of all 3-element subsets that contain at least 2 of $x, y, z$. Thus, $n=|X| \leqslant |Y(x, y, z)| = 1 + C_{3}^{2} C_{33}^{1} = 100$, with equality holding if and only if $X = Y(x, y, z)$. There are $C_{36}^{3}$ such $X = Y(x, y, z)$, and they are different from those in case (I).
In summary, the maximum value of $n$ is 100, and when $n$ reaches its maximum value, there are $33 C_{36}^{3} + C_{36}^{3} = 34 C_{36}^{3}$ different $X$.
| 9
|
1.3. A game of Jai Alai has eight players and starts with players $P_{1}$ and $P_{2}$ on court and the other players $P_{3}, P_{4}, P_{5}, P_{6}, P_{7}, P_{8}$ waiting in a queue. After each point is played, the loser goes to the end of the queue; the winner adds 1 point to his score and stays on the court; and the player at the head of the queue comes on to contest the next point. Play continues until someone has scored 7 points. At that moment, we observe that a total of 37 points have been scored by all eight players. Determine who has won and justify your answer.
|
P_{4}
|
1.3 Each time a player loses a match, he has to wait six games before his turn comes again. If $x$ is the number of games before his first turn, then the player will win if $x+7 r+7=37$, where $r \geq 0$ is an integer and $0 \leq x \leq 6$. Here $r$ counts the number of times he lost. From this, we obtain $x=2$ and $r=4$. Thus the second player in the queue wins. That is $P_{4}$ wins.
| 2.67
|
4. Find the product of all roots of the equation $z^{3}+|z|^{2}=10 i$.
Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.
|
-5+10i
|
4. From $z^{3}=-|z|^{2}+10 i$ we get $z^{3}=-|z|^{2}-10 i$, then $|z|^{6}=|z|^{4}+100$, which means $|z|^{2}=$ 5 , so the original equation becomes $z^{3}+5-10 i=0$, thus the product of all roots is $-5+10 i$.
| 4
|
8. In a regular tetrahedron \(ABCD\) with edge length 1, two tangent spheres are placed inside, one of which is tangent to the three faces passing through point \(A\), and the other is tangent to the three faces passing through point \(B\). Then the minimum value of the sum of their radii is \(\qquad\)
|
\frac{\sqrt{6}-1}{5}
|
8. $\frac{\sqrt{6}-1}{5}$.
Let the centers of the two spheres be $P, Q$, and their radii be $x, y$, respectively. Without loss of generality, assume that sphere $P$ is tangent to the three faces passing through point $A$, and sphere $Q$ is tangent to the three faces passing through point $B$, then $A P=3 x, B Q=3 y$.
Let the projections of $P, Q$ on the plane $A B C$ be $M, N$, respectively, then
$$
M N=\sqrt{(x+y)^{2}-(x-y)^{2}}=2 \sqrt{x y} .
$$
Let the projections of $M, N$ on the line $A B$ be $U, V$, respectively, then $A M=2 \sqrt{2} x, M U=\sqrt{2} x$, $A U=\sqrt{6} x, B N=2 \sqrt{2} y, N V=\sqrt{2} y, B V=\sqrt{6} y$. In the right trapezoid $M N U V$, we have $M N^{2}=$ $(M U-N V)^{2}+U V^{2}$, so
$$
4 x y=(\sqrt{2} x-\sqrt{2} y)^{2}+(1-\sqrt{6} x-\sqrt{6} y)^{2},
$$
Simplifying, we get
$$
12 x y=8(x+y)^{2}-2 \sqrt{6}(x+y)+1 .
$$
By the AM-GM inequality, we have $12 x y \leqslant 3(x+y)^{2}$, substituting into the above equation, we solve to get $x+y \geqslant \frac{\sqrt{6}-1}{5}$. The equality can clearly be achieved. Therefore, the minimum value sought is $\frac{\sqrt{6}-1}{5}$.
| 8
|
3.2. A quadrilateral $ABCD$ is inscribed in a circle $\omega$ such that $AB = AD$ and $BC = CD$ (a deltoid). It turns out that the radius of the inscribed circle of triangle $ABC$ is equal to the radius of the circle that touches the smaller arc $BC$ of circle $\omega$ and the side $BC$ at its midpoint (see Fig. 3). Find the ratio of the side $AB$ to the radius of the inscribed circle of triangle $ABC$.
|
6
|
3.2. Let $I$ be the center of the inscribed circle of triangle $ABC$, $P$ the point of tangency of this inscribed circle with side $AB$, $M$ the midpoint of side $AB$, and $Q$ the midpoint of arc $AB$ (see Fig. 5).
Note that triangle $IPB$ is isosceles and right-angled. Moreover, by the trident theorem, triangle $IQB$ is also isosceles. Therefore, $\angle QPB = \angle QPI = 135^{\circ}$, and thus $\angle MPQ = 45^{\circ}$. It is easy to see that $\angle QMP = 90^{\circ}$, so triangle $QMP$ is isosceles. Therefore, $MP = MQ$.
Thus, the ratio of side $AB$ to the radius is $2 \cdot (MP + PB) / PI = 6$.
| 4.24
|
60th Putnam 1999 Problem A4 Let a ij = i 2 j/(3 i (j 3 i + i 3 j )). Find ∑ a ij where the sum is taken over all pairs of integers (i, j) with i, j > 0.
|
\frac{9}{32}
|
Let b i = i/3 i , then a ij = b i 2 b j (b i + b j ). Let the sum be k. Then k = ∑ a ij = 1/2 ∑ (a ij + a ji ) = 1/2 ∑ b i b j . We have the familiar 1 + 2x + 3x 2 + ... = 1/(1 - x) 2 , so x + 2x 2 + 3x 3 + ... = x/(1 - x) 2 , and hence ∑ b i = 1/3 (2/3) -2 = 3/4. So k = 1/2 (3/4) 2 = 9/32. 60th Putnam 1999 © John Scholes [email protected] 14 Dec 1999
| 6
|
Consider arrangements of the $9$ numbers $1, 2, 3, \dots, 9$ in a $3 \times 3$ array. For each such arrangement, let $a_1$, $a_2$, and $a_3$ be the medians of the numbers in rows $1$, $2$, and $3$ respectively, and let $m$ be the median of $\{a_1, a_2, a_3\}$. Let $Q$ be the number of arrangements for which $m = 5$. Find the remainder when $Q$ is divided by $1000$.
|
360
|
Assume that $5 \in \{a_1, a_2, a_3\}$, $m \neq 5$, and WLOG, $\max{(a_1, a_2, a_3)} = 5$. Then we know that the other two medians in $\{a_1, a_2, a_3\}$ and the smallest number of rows 1, 2, and 3 are all less than 5. But there are only 4 numbers less than 5 in $1, 2, 3, \dots, 9$, a Contradiction. Thus, if $5 \in \{a_1, a_2, a_3\}$, then $m = 5$.
WLOG, assume $5$ is in the upper left corner. One of the two other values in the top row needs to be below $5$, and the other needs to be above $5$. This can be done in $4\cdot4\cdot2=32$ ways.
The other $6$ can be arranged in $6!=720$ ways.
Finally, accounting for when $5$ is in every other space, our answer is $32\cdot720\cdot9$, which is $207360$. But we only need the last $3$ digits, so $\boxed{360}$ is our answer.
~Solution by SuperSaiyanOver9000, mathics42, edited by zhaohm
Alternative Proof
Claim: As long as one median is equal to $5,$ the overall median is equal to $5.$
Proof: Notice that to obtain a median of $5,$ we need one number greater and one number lesser than $5$ along with $5.$
Thus, we remain with 3 numbers greater than $5$ and 3 less than $5,$ meaning that the overall median, no matter the distribution, of the remaining two rows must be $5.$
mathboy282
| 3.4
|
10.4. A $100 \times 100$ grid is given, with cells colored black and white. In each column, there are an equal number of black cells, while in each row, the number of black cells is different. What is the maximum possible number of pairs of adjacent cells of different colors? (I. Bogdanov)
|
14751
|
Answer. $6 \cdot 50^{2}-5 \cdot 50+1=14751$ pairs.
Solution. Let the side length of the table be $2 n = 100$ (so $n=50$) and number the rows from top to bottom and the columns from left to right with numbers from 1 to $2 n$.
In each row, there can be from 0 to $2 n$ black cells. Since the number of black cells in all rows is different, these numbers are all numbers from 0 to $2 n$, except one (say, except $k$). Then the total number of black cells is $(0+1+\ldots+2 n)-k=2 n^{2}+n-k$. On the other hand, since the number of cells in all columns is the same, the total number of black cells must be divisible by $2 n$. Therefore, $k=n$, and in all columns there are $2 n^{2} / (2 n) = n$ black cells.
Now let's estimate the number of pairs of adjacent cells of different colors, considering separately pairs of cells adjacent horizontally and vertically.
If there are $i \leqslant n-1$ black cells in a row, then they can participate in no more than $2 i$ horizontal pairs. If there are $i \geqslant n+1$ black cells in a row, the same reasoning can be applied to the white cells, of which there are $2 n-i \leqslant n-1$. Therefore, the number of horizontal pairs of different colors is no more than $2 \cdot(2 \cdot 0+2 \cdot 1+\ldots+2 \cdot(n-1))=2 n(n-1)$.
Now let's estimate the number of vertical pairs. Consider any row with an even number from 2 to $2(n-1)$; let there be $i$ black cells in it. Then either in the row above or in the row below it, the number of black cells is not equal to $100-i$; therefore, one of the vertical pairs in which the cells of our row participate will be of the same color. Therefore, there are at least $n-1$ same-color vertical pairs. Since the total number of vertical pairs is $2 n(2 n-1)$, the number of different-color vertical pairs is no more than $2 n(2 n-1)-(n-1)$. Therefore, the total number of different-color pairs is no more than $2 n(n-1)+\left(4 n^{2}-3 n+1\right)=6 n^{2}-5 n+1=14751$.
It remains to provide an example in which the specified number of pairs is achieved. Draw a diagonal from the upper left corner to the lower right corner in our $2 n \times 2 n$ table. All cells lying on or below the diagonal will be painted black if they are in even rows, and white otherwise (coloring "by rows"). All cells lying above the diagonal will be painted black if the sum of their row and column numbers is even, and white otherwise (checkerboard coloring). An example of such a coloring for $n=4$ is shown in Fig. 3. It is easy to verify that in each column there are exactly $n$ black cells, in the $2 i$-th row there are $n+i$ black cells, and in the $(2 i-1)$-th row there are $-n-i$ black cells. Moreover, all the estimates above are achieved.
Comment. Only the answer - 0 points.
Only the answer and a correct example - 2 points.
Only the proof of the exact estimate - 4 points.
Proof of the exact estimate only for the number of vertical or only for the number of horizontal different-color pairs - 2 points (can be combined with points for a correct example).
Proved that there is no row containing exactly 50 black cells - 1 point, if there are no other significant advances in the work (otherwise this point is not added).
| 8.67
|
14. As shown in the figure, there are four shapes made up of six different building blocks. The six blocks represent six different single-digit numbers. Three blocks forming a shape represent a three-digit number. 523, 426, 376 correspond to the first three figures below (note: they may not correspond in order, i.e., 523 does not necessarily correspond to the first figure). What number does the fourth figure represent? $\qquad$
(1)
(2)
(3)
(4)
|
325
|
Answer: 325
Explanation: The three given numbers are $523, 426, 376$. The tens place has two identical 2s, and the units place has two identical 6s. From the first three figures, the vertical "one" shaped block represents the number 6; the horizontal "L" shaped block represents the number 2. Therefore, the first figure represents 426, the second figure represents 376, and the third figure represents 523. So, the fourth figure represents 325.
| 2
|
4. A number, its fractional part, integer part, and itself form a geometric sequence, then the number is
保留源文本的换行和格式,所以翻译结果如下:
4. A number, its fractional part, integer part, and itself form a geometric sequence, then the number is
|
\frac{1+\sqrt{5}}{2}
|
$$
x=\frac{1+\sqrt{5}}{2}
$$
4. 【Analysis and Solution】Let the number be $x$, then its integer part is $[x]$, and the fractional part is $x-[x]$. From the given, we have $x=(x-[x])=[x]^{2}$, where $[x]>0, 0<x-[x]<1$. Solving this, we get $x=\frac{1+\sqrt{5}}{2}[x]$. From $0<x-[x]<1$, we know that $0<\frac{\sqrt{5}-1}{2}[x]<1, 0<[x]<\frac{1+\sqrt{5}}{2}<2$, which means $[x]=1, x=\frac{1+\sqrt{5}}{2}$.
| 4.4
|
[ Law of Sines ] [ Law of Cosines ] In triangle $A B C$, medians $A N$ and $C M$ are drawn, $\angle A B C=120^{\circ}$. The circle passing through points $A, M$ and $N$ also passes through point $C$. The radius of this circle is 7. Find the area of triangle $A B C$.
|
7 \sqrt{3}
|
Prove that the given triangle is isosceles, find $A N$, and to find the sides of the given triangle, apply the Law of Cosines to triangle $A B N$.
## Solution
By the theorem of the midline of a triangle, $M N \| A C$, so $A M N C$ is a trapezoid. Since the trapezoid is inscribed in a circle, it is isosceles. Since $A B=2 \cdot A M=2 \cdot C N=B C$, the triangle $A B C$ is also isosceles, so $\angle B A C=\angle B C A=30^{\circ}$.
If $R$ is the radius of the circle, then
$$
A N=2 R \cdot \sin \angle A C N=2 R \cdot \sin 30^{\circ}=R=7
$$
Let $C N=A M=x$. Then $A B=B C=2 x$. By the Law of Cosines in triangle $A B N$, we have:
$$
A N^{2}=A B^{2}+B N^{2}-2 \cdot A B \cdot B N \cdot \cos 120^{\circ} \text{, or } 49=4 x^{2}+x^{2}+2 x^{2}
$$
From this, we find that $x^{2}=7$. Therefore,
$$
S_{\triangle \mathrm{ABC}}=\frac{1}{2} \cdot A B \cdot B C \cdot \sin \angle A B C=\frac{1}{2} \cdot 2 x \cdot 2 x \cdot \sin 120^{\circ}=2 x^{2} \cdot \frac{\sqrt{3}}{2}=x^{2} \sqrt{3}=7 \sqrt{3}
$$
## Answer
$7 \sqrt{3}$.
| 4
|
15. Each edge of a triangular pyramid (tetrahedron) is equal to $a$. Find the maximum area that the orthogonal projection of this pyramid onto a horizontal plane can have.
|
\frac{a^{2}}{2}
|
15. The orthogonal projection of a tetrahedron can be either a triangle or a quadrilateral. In the first case, a regular tetrahedron is projected into a triangle that coincides with the projection of one of its faces. The largest projection in this case will be when the plane of the face is parallel to the projection plane. The projection will be equal to $\frac{a^{2} \sqrt{3}}{4}$, i.e., the area of a regular triangle. In the second case, a regular tetrahedron is projected into a quadrilateral. To obtain the projection with the largest area, the tetrahedron should be positioned so that its vertices coincide with four vertices of a cube, and its edges coincide with the diagonals of the cube's faces, i.e., the regular tetrahedron should be inscribed in a cube with a side length of $\frac{a \sqrt{2}}{2}$, assuming the edge of the tetrahedron is $a$. Then the projection of the tetrahedron will be a square, the area of which is $\frac{a^{2}}{2}$. Clearly, $\frac{a^{2}}{2} > \frac{a^{2} \sqrt{3}}{4}$, i.e., the orthogonal projection of a regular tetrahedron, when it is projected into a square, will be the largest.
| 6.33
|
6. Let $k$ be a real number, in the Cartesian coordinate system $x O y$ there are two point sets $A=\left\{(x, y) \mid x^{2}+y^{2}=\right.$ $2(x+y)\}$ and $B=\{(x, y) \mid k x-y+k+3 \geqslant 0\}$. If $A \cap B$ is a singleton set, then the value of $k$ is $\qquad$
|
-2 - \sqrt{3}
|
The point set $A$ represents the circle $\odot C:(x-1)^{2}+(y-1)^{2}=2$, and the point set $B$ represents the region below the line $y=k(x+1)+3$. Since the line is tangent to $\odot C$, the distance from the center $C(1,1)$ to the line is
$$
d=\frac{|2 k+2|}{\sqrt{k^{2}+1}}=\sqrt{2} \Rightarrow k^{2}+4 k+1=0 \Rightarrow k=\frac{-4 \pm 2 \sqrt{3}}{2}=-2 \pm \sqrt{3} \text {. }
$$
Combining the graph, we can see that the value of $k$ is $-2-\sqrt{3}$.
| 6
|
2. (24th Canadian Mathematical Olympiad) Solve the equation $x^{2}+\left(\frac{x^{2}}{x+1}\right)^{2}=3$ in the set of complex numbers.
|
\frac{-3 + i\sqrt{3}}{2}, \frac{-3 - i\sqrt{3}}{2}, \frac{1 + \sqrt{5}}{2}, \frac{1 - \sqrt{5}}{2}
|
2. Since $x^{2}-2 \cdot \frac{x^{2}}{x+1}+\left(\frac{x}{x+1}\right)^{2}=\left(x-\frac{x}{x+1}\right)^{2}=\left(\frac{x^{2}}{x+1}\right)^{2}$, the original equation can be transformed into $x^{2}+\left(\frac{x}{x+1}\right)^{2}-2 \cdot$ $\frac{x^{2}}{x+1}+2 \cdot \frac{x^{2}}{x+1}=3$
which simplifies to $\left(\frac{x^{2}}{x+1}\right)^{2}+2 \cdot \frac{x^{2}}{x+1}-3=0$, or $\left(\frac{x^{2}}{x+1}+3\right)\left(\frac{x^{2}}{x+1}-1\right)=0$. Thus, $\frac{x^{2}}{x+1}=-3$ or $\frac{x^{2}}{x+1}=1$. Solving these equations yields:
$$
x_{1}=\frac{1}{2}(-3+\sqrt{3} \mathrm{i}), x_{2}=\frac{1}{2}(-3-\sqrt{3} \mathrm{i}), x_{3}=\frac{1}{2}(1+\sqrt{5}), x_{4}=\frac{1}{2}(1-\sqrt{5}) .
$$
| 2.6
|
55. In a $10 \times 10$ grid (the sides of the cells have a unit length), $n$ cells were chosen, and in each of them, one of the diagonals was drawn and an arrow was placed on this diagonal in one of two directions. It turned out that for any two arrows, either the end of one coincides with the beginning of the other, or the distance between their ends is at least 2. What is the largest $n$ for which this is possible?
|
48
|
55. Answer: when $n=48$.
For each arrow, consider the three-cell corner obtained by removing from a $2 \times 2$ square, centered at the end of the arrow, a $1 \times 1$ square, the diagonal of which is this arrow. Note that such corners do not intersect and are contained within a $12 \times 12$ square. Therefore, there are no more than $12^{2} / 3=48$ such corners.
An example of placing 48 arrows is shown in the figure.
| 5
|
15. Master Wang works in a special position, where he works for 8 consecutive days and then takes 2 consecutive days off. If he is off on this Saturday and Sunday, then, at least how many weeks later will he be off on a Sunday again?
|
7
|
15. At least another 7 weeks
15.【Solution】Let at least $\mathrm{n}$ weeks pass, it is possible to rest on the $\mathrm{n}$th Saturday, or it is also possible not to rest on the $\mathrm{n}$th Saturday (resting for 2 days on Sunday and Monday), the former yields: $7 \mathrm{n}-2=10 \mathrm{~K}+8(1)$, the latter yields: $7 \mathrm{n}-1=10 \mathrm{~K}+8(2)$, where $\mathrm{K}$ is a natural number.
(1) That is, $7 n=10(K+1)$, thus, $n$ is a multiple of 10, at least 10.
(2) That is, $7 n=10 K+9$, it indicates that the unit digit of $7 n$ is 9, so $n=7,17, \cdots$
Therefore, at least another 7 weeks must pass before resting on a Sunday again.
| 2.33
|
The grid below is to be filled with integers in such a way that the sum of the numbers in each row and the sum of the numbers in each column are the same. Four numbers are missing. The number $x$ in the lower left corner is larger than the other three missing numbers. What is the smallest possible value of $x$?
$\textbf{(A) } -1 \qquad \textbf{(B) } 5 \qquad \textbf{(C) } 6 \qquad \textbf{(D) } 8 \qquad \textbf{(E) } 9 \qquad$
|
8
|
The sum of the numbers in each row is $12$. Consider the second row. In order for the sum of the numbers in this row to equal $12$, the two shaded numbers must add up to $13$:
If two numbers add up to $13$, one of them must be at least $7$: If both shaded numbers are no more than $6$, their sum can be at most $12$. Therefore, for $x$ to be larger than the three missing numbers, $x$ must be at least $8$. We can construct a working scenario where $x=8$:
So, our answer is $\boxed{\textbf{(D) } 8}$.
~ihatemath123
| 3.75
|
5 Find all real numbers $a$ such that any positive integer solution of the inequality $x^{2}+y^{2}+z^{2} \leqslant a(x y+y z+z x)$ are the lengths of the sides of some triangle.
|
[1, \frac{6}{5})
|
5. Taking $x=2, y=z=1$, we have $a \geqslant \frac{6}{5}$. Therefore, when $a \geqslant \frac{6}{5}$, the original inequality has integer roots $(2,1,1)$, but $(x, y, z)$ cannot form a triangle, so $a<\frac{6}{5}$.
When $a<1$, $x^{2}+y^{2}+z^{2} \leqslant a(x y+y z+z x)<x y+y z+z x$, which is a contradiction! Hence, $a \geqslant 1$. We now prove that when $1 \leqslant a<\frac{6}{5}$, all positive integer roots of the original inequality can form the sides of a triangle.
First, $(1,1,1)$ is a solution to the original inequality, and they can form a triangle. If the inequality has integer roots $\left(x_{1}, y_{1}, z_{1}\right)$, and they cannot form the sides of a triangle, then, transforming the original equation: (assuming $\left.x_{1} \geqslant y_{1}+z_{1}\right) x^{2}-a(y+z) x+y^{2}+z^{2}-a y z \leqslant 0$.
Consider the function $f(x)=x^{2}-a\left(y_{1}+z_{1}\right) x+y_{1}^{2}+z_{1}^{2}-a y_{1} z_{1}$, its axis of symmetry is $x=$ $\frac{a}{2}\left(y_{1}+z_{1}\right)<\frac{3}{5}\left(y_{1}+z_{1}\right)<y_{1}+z_{1} \leqslant x_{1}$, so $\left(y_{1}+z_{1}, y_{1}, z_{1}\right)$ is also a solution to the original inequality.
Therefore, $a \geqslant \frac{\left(y_{1}+z_{1}\right)^{2}+y_{1}^{2}+z_{1}^{2}}{\left(y_{1}+z_{1}\right) y_{1}+\left(y_{1}+z_{1}\right) z_{1}+y_{1} z_{1}}=u$, then $(u-2) y_{1}^{2}+(3 u-$ 2) $y_{1} z_{1}+(u-2) z_{1}^{2}=0$
Clearly, $u \neq 2$, so $\Delta=(3 u-2)^{2}-4(u-2)^{2} \geqslant 0$, thus $u \geqslant \frac{6}{5}$, then $a \geqslant u \geqslant$ $\frac{6}{5}$, which is a contradiction!
| 5
|
The base of the right parallelepiped $A B C D A 1 B 1 C 1 D 1$ is a square $A B C D$ with a side length of 4, and the length of each lateral edge $A A 1, B B 1, C C 1, D D 1$ is 6. A right circular cylinder is positioned such that its axis lies in the plane $B B 1 D 1 D$, and the points $A 1, C 1, B 1$ and the center $O$ of the square $A B C D$ lie on the lateral surface of the cylinder. Find the radius of the cylinder (find all solutions).
|
$\frac{5}{\sqrt{3}}, 4 \sqrt{\frac{2}{3}}, \frac{20}{3} \sqrt{\frac{2}{11}}$
|
1. Suppose the axis $l$ of the cylinder intersects the line $OB_1$ at some point $K$ (Fig.1), and the line $BB_1$ at point $F$. Let $A_2, B_2, C_2$, and $O_2$ be the projections of points $A, B, C$, and $O$ onto the line $l$, respectively. Then the point $A_2$ coincides with the point $C_2$, and since points $O$ and $B_1$ are equidistant from the axis of the cylinder, $B_1B_2 = OO_2 = R$ (where $R$ is the desired radius of the cylinder), so point $K$ is the midpoint of the segment $OB_1$. Draw a line through point $K$ parallel to $BD$. Let this line intersect the edges $BB_1$ and $DD_1$ at points $N$ and $M$, respectively. Then $N$ and $M$ are the midpoints of these edges. Denote $\angle FKN = \alpha, \angle B_1KN = \beta$. We will assume that $\alpha > 0$ and $\cos \alpha > 0$. Squaring both sides of the obtained equation:
$$
9 \sin^2 \alpha \cos^2 \alpha = 2.9 \sin^2 \alpha (1 - \sin^2 \alpha) = 2
$$
$$
9 \sin^4 \alpha - 9 \sin^2 \alpha + 2 = 0, \left(\sin^2 \alpha - \frac{2}{3}\right)\left(\sin^2 \alpha - \frac{1}{3}\right) = 0
$$
from which $\sin \alpha = \sqrt{\frac{2}{3}}$ or $\sin \alpha = \frac{1}{\sqrt{3}}$. In the first case,
$$
R = \sqrt{2} \sin \alpha + 3 \cos \alpha = \sqrt{2} \cdot \sqrt{\frac{2}{3}} + 3 \cdot \frac{1}{\sqrt{3}} = \frac{5}{\sqrt{3}}
$$
in the second case,
$$
R = \sqrt{2} \sin \alpha + 3 \cos \alpha = \sqrt{2} \cdot \frac{1}{\sqrt{3}} + 3 \cdot \sqrt{\frac{2}{3}} = 4 \sqrt{\frac{2}{3}}
$$
2. Suppose the axis $l$ is parallel to the line $OB_1$ (Fig.2). Then $OB_1$ is a generatrix of the cylinder. Let $A_2, B_2, C_2$, and $O_2$ be the projections of points $A, B, C$, and $O$ onto the line $l$, respectively, and $O_1$ be the center of the square $A_1B_1C_1D_1$. Then the point $A_2$ coincides with the point $C_2$, and since points $O$ and $B_1$ are equidistant from the axis of the cylinder, $B_1B_2 = OO_2 = R$ (where $R$ is the desired radius of the cylinder), the line $O_1C_2$ is perpendicular to the axis $l$ of the cylinder. If the lines $O_1C_2$ and $OB_1$ intersect at point $E$, then $O_1E \perp OB_1$. Denote $\angle OO_1E = \angle BOB_1 = \beta$. Then
$$
OB_1 = \sqrt{BB_1^2 + B_1O_1^2} = \sqrt{36 + 8} = 2\sqrt{11}, \sin \beta = \frac{BB_1}{OB_1} = \frac{6}{2\sqrt{11}} = \frac{3}{\sqrt{11}}
$$
$$
O_1E = OO_1 \cos \beta = 6 \sqrt{\frac{2}{11}}, C_2E = B_1B_2 = R, C_2O_1 = C_2E - O_1E = R - 6 \sqrt{\frac{2}{11}}
$$
From the right triangle $C_1OC_2$ we find that $C_1C_2^2 = O_1C_2^2 + O_1C_1^2$, or
$$
R^2 = \left(R - 6 \sqrt{\frac{2}{11}}\right)^2 + 8
$$
from which $R = \frac{20}{3} \sqrt{\frac{2}{11}}$.
## Answer
$\frac{5}{\sqrt{3}}, 4 \sqrt{\frac{2}{3}}, \frac{20}{3} \sqrt{\frac{2}{11}}$
| 6.5
|
$2.351 A=\frac{x^{8}+x^{4}-2 x^{2}+6}{x^{4}+2 x^{2}+3}+2 x^{2}-2$.
|
A=x^{4}
|
Solution. Let's divide the polynomial $x^{8}+x^{4}-2 x^{6}+6$ by the polynomial $x^{4}+2 x^{2}+3$.
$$
\begin{aligned}
& \begin{array}{r}
-\frac{-2 x^{6}-4 x^{4}-6 x^{2}}{-2 x^{4}+4 x^{2}+6} \\
\frac{2 x^{4}+4 x^{2}+6}{0}
\end{array}
\end{aligned}
$$
Therefore, $A=\frac{\left(x^{4}+2 x^{2}+3\right)\left(x^{4}-2 x^{2}+2\right)}{x^{4}+2 x^{2}+3}+2 x^{2}-2=x^{4}$.
Answer: $A=x^{4}$.
| 2.33
|
80. One day, Xiao Ben told a joke. Except for Xiao Ben himself, four-fifths of the classmates in the classroom heard it, but only three-quarters of the classmates laughed. It is known that one-sixth of the classmates who heard the joke did not laugh. Then, what fraction of the classmates who did not hear the joke laughed?
|
\frac{5}{12}
|
Reference answer: $5 / 12$
| 2.33
|
Example 3 Given a positive integer $n \geqslant 3$, let $d_{1}, d_{2}, \cdots, d_{n}$ be positive integers, whose greatest common divisor is 1, and $d_{i}$ divides $d_{1}+d_{2}+\cdots+d_{n}(i=1,2, \cdots, n)$. Find the smallest positive integer $k$, such that $d_{1} d_{2} \cdots d_{n}$ divides $\left(d_{1}+\right.$ $\left.d_{2}+\cdots+d_{n}\right)^{k}$.
|
n-2
|
Let $d_{1}=1, d_{2}=n-1, d_{3}=d_{4}=\cdots=d_{n}=n$, then $d_{1}+d_{2}+\cdots+d_{n}=1+$ $(n-1)+(n-2) \cdot n=(n-1) n$, which is divisible by every $d_{i}(i=1,2, \cdots, n)$, and the greatest common divisor of $d_{1}, d_{2}, \cdots, d_{n}$ is 1, at this time $d_{1} d_{2} \cdots d_{n}=(n-1) n^{n-2}$. If $d_{1} d_{2} \cdots d_{n}$ divides $\left(d_{1}+\cdots+d_{n}\right)^{k}$, i.e., $(n-1) n^{n-2} \mid[(n-1) n]^{k}$, by $(n, n-1)=1$ we get $k \geqslant n-2$.
Conversely, we prove: If the greatest common divisor of $d_{1}, d_{2}, \cdots, d_{n}$ is 1, and $d_{i}$ divides $\left(d_{1}+d_{2}+\cdots+d_{n}\right)$ $(i=1,2, \cdots, n)$, then $d_{1} d_{2} \cdots d_{n} \mid\left(d_{1}+d_{2}+\cdots+d_{n}\right)^{n-2}$.
In fact, let $p$ be any prime factor of $d_{1} d_{2} \cdots d_{n}$, then there exists a positive integer $k$, such that at least one of $d_{1}, d_{2}, \cdots, d_{n}$ is divisible by $p^{k}$, and no $d_{1}, d_{2}, \cdots, d_{n}$ is divisible by $p^{k+1}$. Thus, by $d_{i} \mid\left(d_{1}+d_{2}+\cdots+d_{n}\right)$ we get $p^{k} \mid\left(d_{1}+d_{2}+\cdots+d_{n}\right)$, hence $p^{k(n-2)} \mid\left(d_{1}+d_{2}+\cdots+d_{n}\right)^{n-2}$. Since the greatest common divisor of $d_{1}, d_{2}, \cdots, d_{n}$ is 1, there must be some $d_{j}$ not divisible by $p$. Also, since $p$ divides $d_{1}+$ $d_{2}+\cdots+d_{n}$, at least two of $d_{1}, d_{2}, \cdots, d_{n}$ are not divisible by $p$, so the highest power of $p$ dividing $d_{1} d_{2} \cdots d_{n}$ is at most $p^{k(n-2)}$. Repeating the above discussion for each prime factor of $d_{1}, d_{2}, \cdots, d_{n}$, we know that $d_{1} d_{2} \cdots$ $d_{n}$ divides $\left(d_{1}+d_{2}+\cdots+d_{n}\right)^{n-2}$.
In summary, the smallest positive integer $k=n-2$.
| 5
|
5. Teresa the bunny has a fair 8 -sided die. Seven of its sides have fixed labels $1,2, \ldots, 7$, and the label on the eighth side can be changed and begins as 1 . She rolls it several times, until each of $1,2, \ldots, 7$ appears at least once. After each roll, if $k$ is the smallest positive integer that she has not rolled so far, she relabels the eighth side with $k$. The probability that 7 is the last number she rolls is $\frac{a}{b}$, where $a$ and $b$ are relatively prime positive integers. Compute $100 a+b$.
|
104
|
Answer:
104
Solution 1: Let $n=7$ and $p=\frac{1}{4}$.
Let $q_{k}$ be the probability that $n$ is the last number rolled, if $k$ numbers less than $n$ have already bee rolled. We want $q_{0}$ and we know $q_{n-1}=1$.
We have the relation
$$
q_{k}=(1-p) \frac{k}{n-1} q_{k}+\left[1-(1-p) \frac{k+1}{n-1}\right] q_{k+1} .
$$
This rearranges to
$$
\left[1-(1-p) \frac{k}{n-1}\right] q_{k}=\left[1-(1-p) \frac{k+1}{n-1}\right] q_{k+1} .
$$
This means that the expression on the LHS does not depend on $k$, so
$$
[1-0] \cdot q_{0}=[1-(1-p)] \cdot q_{n-1}=p .
$$
Solution 2: For a given sequence of Teresa's rolls, let $x_{i}$ be the $i$ th distinct number rolled. We want to compute the probability that $x_{7}=7$.
For a given index $i$, we say that $x_{i}$ is correct if $x_{i}$ is the least positive integer not in $\left\{x_{1}, \ldots, x_{i-1}\right\}$. Note that the probability of a given sequence $x_{1}, \ldots, x_{7}$ depends only on the number of correct $x_{i}$, since the probability of rolling the correct number on a given roll is higher by a factor of 2 .
Now, suppose $x_{7}=7$. Consider $x_{i}^{\prime}=x_{i-1}+1$ for $1<i \leq 7$, and $x_{1}^{\prime}=1$. Note that this operation on sequences $x_{1}, \ldots, x_{7}$ pairs sequences ending in 7 with sequences starting with 1 . Additionally, we have that $x_{7}$ and $x_{1}^{\prime}$ are both correct, and that $x_{i}^{\prime}$ is correct if and only if $x_{i-1}$ is correct. Thus $x_{1}, \ldots, x_{7}$ and $x_{1}^{\prime}, \ldots, x_{7}^{\prime}$ have the same probability.
So, we conclude that the probability of $x_{7}=7$ is the same as the probability of $x_{1}=1$. But this is just $\frac{1}{4}$.
| 5
|
64. 1 9 Choose 4 different digits from these 9 numbers, form a four-digit number, so that this four-digit number can be divided by the 5 numbers not selected, but cannot be divided by the 4 selected numbers. Then, this four-digit number is . $\qquad$
|
5936
|
Answer: 5936
| 4.75
|
Example 3 (1) Given the geometric sequences $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$ satisfy:
$$
\begin{array}{l}
a_{1}=a>0, b_{1}-a_{1}=1, \\
b_{2}-a_{2}=2, b_{3}-a_{3}=3 .
\end{array}
$$
If the sequence $\left\{a_{n}\right\}$ exists and is unique, find the value of $a$.
(2) Do there exist two geometric sequences $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$ such that $b_{1}-a_{1}, b_{2}-a_{2}, b_{3}-a_{3}, b_{4}-a_{4}$ form an arithmetic sequence with a non-zero common difference? If they exist, find the general terms of $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$; if not, explain the reason.
|
\frac{1}{3}
|
【Analysis】"The common ratio of a geometric sequence cannot be 0" is a common knowledge. If this is asked directly, it would become a "junk question". However, if this concept is appropriately hidden in the problem-solving process, it could become a good question.
This problem is from the 2011 Jiangxi Province College Entrance Examination Mathematics Test, which hides the concept that "the common ratio of a geometric sequence cannot be 0" in the problem statement. According to the statistics from the grading group, the vast majority of candidates attributed the "uniqueness" of the problem to whether the discriminant is zero, which did not succeed, resulting in a very low score rate for the problem.
Solution (1) Let the common ratio of $\left\{a_{n}\right\}$ be $q$. Then
$$
b_{1}=1+a, b_{2}=2+a q, b_{3}=3+a q^{2} \text {. }
$$
Since $b_{1} 、 b_{2} 、 b_{3}$ form a geometric sequence, we have
$$
\begin{array}{l}
(2+a q)^{2}=(1+a)\left(3+a q^{2}\right) \\
\Rightarrow a q^{2}-4 a q+3 a-1=0 .
\end{array}
$$
Since $a>0 \Rightarrow \Delta=4 a^{2}+4 a>0$
$\Rightarrow$ the equation has two distinct real roots.
Furthermore, since $\left\{a_{n}\right\}$ exists and is unique, the equation must have one root as 0. Substituting $q=0$ into the equation gives $a=\frac{1}{3}$.
(2) Assume there exist two geometric sequences $\left\{a_{n}\right\} 、\left\{b_{n}\right\}$ that satisfy the conditions, with the common ratio of $\left\{a_{n}\right\}$ being $q_{1}$ and the common ratio of $\left\{b_{n}\right\}$ being $q_{2}$. Then
$$
\begin{array}{l}
b_{2}-a_{2}=b_{1} q_{2}-a_{1} q_{1}, \\
b_{3}-a_{3}=b_{1} q_{2}^{2}-a_{1} q_{1}^{2}, \\
b_{4}-a_{4}=b_{1} q_{2}^{3}-a_{1} q_{1}^{3} .
\end{array}
$$
By the problem's conditions, we have
$$
\begin{array}{l}
2\left(b_{1} q_{2}-a_{1} q_{1}\right) \\
=b_{1}-a_{1}+\left(b_{1} q_{2}^{2}-a_{1} q_{1}^{2}\right), \\
2\left(b_{1} q_{2}^{2}-a_{1} q_{1}^{2}\right) \\
=b_{1} q_{2}-a_{1} q_{1}+\left(b_{1} q_{2}^{3}-a_{1} q_{1}^{3}\right), \\
\text { i.e., }\left\{\begin{array}{l}
b_{1}\left(q_{2}-1\right)^{2}-a_{1}\left(q_{1}-1\right)^{2}=0, \\
b_{1} q_{2}\left(q_{2}-1\right)^{2}-a_{1} q_{1}\left(q_{1}-1\right)^{2}=0 .
\end{array}\right.
\end{array}
$$
(1) $\times q_{2}$-(2) gives
$$
a_{1}\left(q_{1}-q_{2}\right)\left(q_{1}-1\right)^{2}=0 \text {. }
$$
Since $a_{1} \neq 0$, we have $q_{1}=q_{2}$ or $q_{1}=1$.
When $q_{1}=q_{2}$, from equations (1) and (2) we get
$$
b_{1}=a_{1} \text { or } q_{1}=q_{2}=1 \text {, }
$$
In this case, $\left(b_{2}-a_{2}\right)-\left(b_{1}-a_{1}\right)=0$ contradicts the condition that the common difference is not 0.
When $q_{1}=1$, from equations (1) and (2) we get $b_{1}=0$ or $q_{2}=$ 1, in which case $\left(b_{2}-a_{2}\right)-\left(b_{1}-a_{1}\right)=0$ also contradicts the condition that the common difference is not 0.
Therefore, there do not exist two geometric sequences $\left\{a_{n}\right\} 、\left\{b_{n}\right\}$ that satisfy the conditions.
In "Dream of the Red Chamber," it is said that the magic jade is "coming without a trace, going without a trace, leaning on an ancient pine under the Green Peak; to seek it, mountains are many, but a smile greets us at the door," describing such a realm. And the problem setters often need to discover and find such a "magic jade" in the structure of mathematics.
| 5
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.